Giải mục 2 trang 34 Chuyên đề học tập Toán 10 - Cánh diềuTừ các đẳng thức như Tổng hợp đề thi học kì 1 lớp 10 tất cả các môn - Cánh diều Toán - Văn - Anh - Lí - Hóa - Sinh - Sử - Địa...
Lựa chọn câu để xem lời giải nhanh hơn
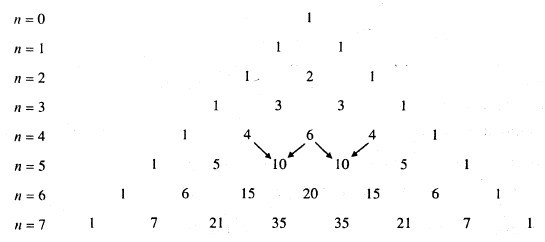
Luyện tập Sử dụng tam giác Pascal để khai triển các biểu thức sau: a) \({(x + y)^7}\) b) \({(x - 2)^7}\) Phương pháp giải: Tam giác Pascal
Lời giải chi tiết: Theo công thức nhị thức Newton, ta có: \({(3x + 2)^9} = C_9^0{\left( {3x} \right)^9} + C_9^1{\left( {3x} \right)^8}2 + ... + C_9^k{\left( {3x} \right)^{9 - k}}{2^k} + ... + C_9^8\left( {3x} \right){2^8} + C_9^9{2^9}\) Số hạng chứa \({x^2}\) ứng với \(9 - k = 2\) hay \(k = 7\). Do đó hệ số của \({x^2}\) là \(C_9^7{3^2}{2^7} = 36.9.128 = 41472\)
 Chia sẻ Bình luận
Tham Gia Group Dành Cho 2K9 Chia Sẻ, Trao Đổi Tài Liệu Miễn Phí
|
