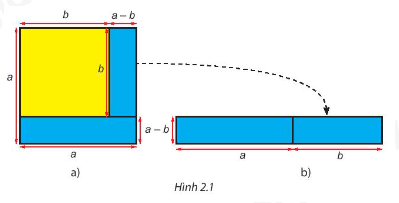
Giải mục 2 trang 30,31 SGK Toán 8 tập 1 - Kết nối tri thứcQuan sát Hình 2.1 a) Tính diện tích của phần hình màu xanh ở Hình 2.1a. b) Tính diện tích hình chữ nhật màu xanh ở Hình 2.1b. c) Có nhận xét gì về diện tích của hai hình ở câu a và câu b? Tổng hợp đề thi học kì 1 lớp 8 tất cả các môn - Kết nối tri thức Toán - Văn - Anh - Khoa học tự nhiên
Lựa chọn câu để xem lời giải nhanh hơn
HĐ1 Video hướng dẫn giải Quan sát Hình 2.1 a) Tính diện tích của phần hình màu xanh ở Hình 2.1a. b) Tính diện tích hình chữ nhật màu xanh ở Hình 2.1b. c) Có nhận xét gì về diện tích của hai hình ở câu a và câu b? Phương pháp giải: Diện tích hình chữ nhật = chiều dài . chiều rộng Lời giải chi tiết: a) Diện tích của phần hình màu xanh ở Hình 2.1a là: \({a^2} - {b^2}\). b) Diện tích hình chữ nhật màu xanh ở Hình 2.1b là: \(\left( {a + b} \right)\left( {a - b} \right)\). c) Diện tích hai hình ở câu a và b bằng nhau. HĐ2 Video hướng dẫn giải Với hai số a,b bất kì, thực hiện phép tính \(\left( {a + b} \right)\left( {a - b} \right)\). Từ đó rút ra liên hệ giữa \({a^2} - {b^2}\) và \(\left( {a + b} \right)\left( {a - b} \right)\). Phương pháp giải: Muốn nhân hai đa thức ta nhân mỗi hạng tử của đa thức này với từng hạng tử của đa thức kia rồi cộng các kết quả với nhau. Lời giải chi tiết: \(\left( {a + b} \right)\left( {a - b} \right) = a.a - ab + b.a - b.b = {a^2} - {b^2} + \left( { - ab + ba} \right) = {a^2} - {b^2}\) Từ đó ta được \({a^2} - {b^2} = \left( {a + b} \right)\left( {a - b} \right)\) Luyện tập 2 Video hướng dẫn giải a) Tính nhanh \({99^2} - 1\) b) Viết \({x^2} - 9\) dưới dạng tích. Phương pháp giải: Sử dụng hằng đẳng thức \({a^2} - {b^2} = \left( {a + b} \right)\left( {a - b} \right)\) Lời giải chi tiết: a) \({99^2} - 1 = {99^2} - {1^2} = \left( {99 + 1} \right).\left( {99 - 1} \right) = 100.98 = 9800.\) b) \({x^2} - 9 = {x^2} - {3^2} = \left( {x + 3} \right).\left( {x - 3} \right)\) Vận dụng Video hướng dẫn giải Ở bài toán mở đầu, em hãy giải thích xem bạn đó tính nhanh như thế nào. Phương pháp giải: Sử dụng hằng đẳng thức \({a^2} - {b^2} = \left( {a + b} \right)\left( {a - b} \right)\) Lời giải chi tiết: \(198.202 = \left( {200 - 2} \right).\left( {200 + 2} \right) = {200^2} - {2^2} = 40000 - 4 = 39996.\)
|