Giải mục 2 trang 24, 25, 26 SGK Toán 8 tập 2 – Chân trời sáng tạo

HĐ2

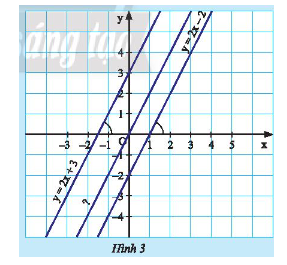
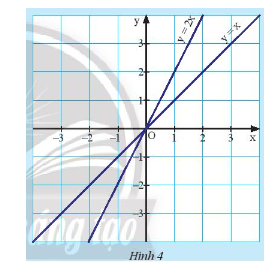
Quan sát Hình 3.

a) So sánh hệ số góc của hai đường thẳng:

\(d:y = 2x + 3\) và \(d':y = 2x - 2\).

Nêu nhận xét về vị trí giữa hai đường thẳng này.

b) Tìm đường thẳng \(d''\) đi qua gốc tọa độ \(O\) và song song với đường thẳng \(d\).

Phương pháp giải:

- Hệ số \(a\) là hệ số góc của đường thẳng \(y = ax + b\left( {a \ne 0} \right)\).

- Đường thẳng đi qua gốc tọa độ có dạng \(y = ax\left( {a \ne 0} \right)\).

Lời giải chi tiết:

a) Đường thẳng \(d:y = 2x + 3\) có hệ số góc là \(a = 2\).

Đường thẳng \(d':y = 2x - 2\) có hệ số góc là \(a' = 2\).

Hệ số góc của hai đường thẳng \(d\) và \(d'\) bằng nhau.

Từ đồ thị ta thấy, hai đường thẳng \(d\) và \(d'\) song song với nhau.

b) Đường thẳng \(d''\) đi qua gốc tọa độ \(O\) nên có dạng \(y = a''x\).

Từ đồ thị ta thấy, \(d''\) đi qua điểm \(\left( {1;2} \right)\) nên ta có:

\(2 = 1.a'' \Rightarrow a'' = 2\).

Do đó, đường thẳng \(d''\) là \(y = 2x\).

HĐ3

Quan sát Hình 4.

a) Tìm giao điểm của hai đường thẳng \(d:y = 2x\)  và \(d':y = x\).

b) Nêu nhận xét về hai đường thẳng có hệ số góc khác nhau.

c) Cho đường thẳng \(d':y = ax + b\) và cho biết \(d''\) cắt \(d\). Hệ số góc \(a\) của đường thẳng \(d''\) có thể nhận giá trị nào?

Phương pháp giải:

- Giao điểm của hai đường thẳng là điểm chung mà cả hai đường thẳng đều đi qua.

- Hệ số \(a\) là hệ số góc của đường thẳng \(y = ax + b\left( {a \ne 0} \right)\).

- Hai đường thẳng phân biệt song song với nhau nếu hệ số góc của chúng bằng nhau.

Lời giải chi tiết:

a) Đường thẳng \(d:y = 2x\)  và \(d':y = x\) đều có dạng \(y = ax\) nên giao điểm của hai đường thẳng là \(O\left( {0;0} \right)\) (cả hai đường thẳng đều đi qua điểm \(O\left( {0;0} \right)\).

b)

- Hệ số góc của đường thẳng \(d:y = 2x\) là\(a = 2\).

- Hệ số góc của đường thẳng \(d':y = x\) là\(a = 1\).

Hai đường thẳng có hệ số góc khác nhau thì cắt nhau.

c) Vì \(d\) và \(d''\) cắt nhau nên chúng không thể song song với nhau hoặc trùng nhau. Do đó, hệ số góc của \(d\) và \(d''\) phải khác nhau. Khi đó, hệ số góc của \(d''\) khác 2.

TH2

Hãy chỉ ra ba cặp đường thẳng cắt nhau và các cặp đường thẳng song song với nhau trong các đường thẳng sau:

\({d_1}:y = 3x\); \({d_2}:y =  - 7x + 9\); 

\({d_3}:y = 3x - 0,8\); \({d_4}:y =  - 7x - 1\); 

\({d_5}:y = \sqrt 2 x + 10\); \({d_6}:y = \sqrt 2 x + \sqrt {10} \)

Phương pháp giải:

- Hệ số \(a\) là hệ số góc của đường thẳng \(y = ax + b\left( {a \ne 0} \right)\).

- Hai đường thẳng phân biệt song song với nhau khi có hệ số góc bằng nhau.

- Hai đường thẳng cắt nhau khi có hệ số góc khác nhau.

Lời giải chi tiết:

Hệ số góc của đường thẳng \({d_1}:y = 3x\) là \(a = 3\);

Hệ số góc của đường thẳng \({d_2}:y =  - 7x + 9\) là \(a =  - 7\);

Hệ số góc của đường thẳng \({d_3}:y = 3x - 0,8\) là \(a = 3\);

Hệ số góc của đường thẳng \({d_4}:y =  - 7x - 1\) là \(a =  - 7\);

Hệ số góc của đường thẳng \({d_5}:y = \sqrt 2 x + 10\) là \(a = \sqrt 2 \);

Hệ số góc của đường thẳng \({d_6}:y = \sqrt 2 x + \sqrt {10} \) là \(a = \sqrt 2 \);

- Các cặp đường thẳng song song là:

\({d_1}:y = 3x\) và \({d_3}:y = 3x - 0,8\) vì đều có hệ số góc \(a = 3\) và chúng phân biệt với nhau do chúng cắt \(Oy\) tại hai điểm phân biệt.

\({d_2}:y =  - 7x + 9\) và \({d_4}:y =  - 7x - 1\) vì đều có hệ số góc \(a =  - 7\)và chúng phân biệt với nhau do chúng cắt \(Oy\) tại hai điểm phân biệt.

\({d_5}:y = \sqrt 2 x + 10\) và \({d_6}:y = \sqrt 2 x + \sqrt {10} \) vì đều có hệ số góc \(a = \sqrt 2 \)và chúng phân biệt với nhau do chúng cắt \(Oy\) tại hai điểm phân biệt.

- Ba cặp đường thẳng cắt nhau là:

\({d_1}:y = 3x\) và \({d_4}:y =  - 7x - 1\) vì có hệ số góc khác nhau \(\left( {3 \ne  - 7} \right)\).

\({d_2}:y =  - 7x + 9\) và \({d_6}:y = \sqrt 2 x + \sqrt {10} \) vì có hệ số góc khác nhau \(\left( { - 7 \ne \sqrt 2 } \right)\).

\({d_3}:y = 3x - 0,8\) và \({d_5}:y = \sqrt 2 x + 10\) vì có hệ số góc khác nhau \(\left( {3 \ne \sqrt 2 } \right)\).

VD2

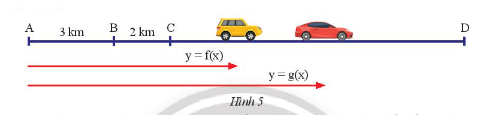
Hai ô tô khởi cùng lúc và cùng vận tốc 50 \(km/h\), một ô tô bắt đầu từ \(B\), một ô tô bắt đầu từ \(C\) và cùng đi về phía \(D\).

a) Viết công thức của hai hàm số biểu thị khoảng cách từ \(A\) đến mỗi xe sau \(x\) giờ.

b) Chứng tỏ đồ thị của hai hàm số trên là hai đường thẳng song song.

Phương pháp giải:

- Quãng đường vật đi được trong khoảng thời gian \(t\left( h \right)\) với vận tốc \(v\left( {km/h} \right)\) là:

\(s = v.t\)

- Khoảng cách của xe sau \(t\left( h \right)\) với một điểm là:

\(y = {y_0} + v.t\)

Với \({y_0}\) là khoảng cách của xe với điểm ở thời điểm ban đầu, \(v\) là vận tốc của xe, t là thời gian xe đã đi.

- Hai hàm số có đồ thị là hai đường thẳng song song nếu chúng phân biệt và có hệ số góc bằng nhau.

Lời giải chi tiết:

a)

- Quãng đường xe ô tô khởi hành từ \(B\) đi được sau khoảng thời gian \(x\left( h \right)\) với vận tốc 50 km/h là: \(s = v.t = 50.x\)

Khi đó, công thức biểu thị khoảng cách từ điểm \(A\) đến xe là:

\(y = {y_0} + v.t = 3 + 50.x\).

- Quãng đường xe ô tô khởi hành từ \(C\) đi được sau khoảng thời gian \(x\left( h \right)\) với vận tốc 50 km/h là: \(s = v.t = 50.x\)

Khi đó, công thức biểu thị khoảng cách từ điểm \(A\) đến xe là:

\(y = {y_0} + v.t = 5 + 50.x\).

b) Đồ thị của hai hàm số trên là hai đường thẳng phân biệt vì cắt \(Oy\) tại hai điểm phân biệt.

Hai đường thẳng đó song song với nhau vì hệ số góc của hai đường thẳng này bằng nhau (đều có \(a = 50\)).