Giải mục 2 trang 13, 14, 15 SGK Toán 8 tập 1– Chân trời sáng tạo

HĐ2

Hình hộp chữ nhật \(A\) có chiều rộng \(2x\), chiều dài và chiều cao đề gấp \(k\) lần chiều rộng (Hình 2).

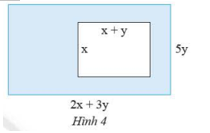
a) Tính diện tích đáy của \(A\).

b) Tính thể tích của \(A\).

Phương pháp giải:

Để nhân hai đơn thức, ta nhận các hệ số với nhau, nhân các lũy thừa cùng biến, rồi nhân các kết quả đó với nhau.

a) Diện tích đáy của hình hộp chữ nhật: \(S = ab\)

b) Thể tích của hình hộp chữ nhật: \(V = abc\)

trong đó \(a\), \(b\), \(c\) là chiều dài, chiều rộng, chiều cao của hình hộp chữ nhật.

Lời giải chi tiết:

a) Chiều dài, chiều cao hình hộp chữ nhật \(A\) là: \(2xk\)

Diện tích đáy của hình hộp chữ nhật \(A\) là: \(2xk.2x = 4k{x^4}\)

b) Thể tích của hình hộp chữ nhật \(A\) là: \(2xk.2x.2xk = 8{k^2}{x^3}\)

TH 2

Thực hiện các phép nhân đơn thức sau:

a) \(\left( {4{x^3}} \right).\left( { - 6{x^3}y} \right)\)                     

b) \(\left( { - 2y} \right).\left( { - 5x{y^2}} \right)\)                      

c) \({\left( { - 2a} \right)^3}.{\left( {2ab} \right)^2}\)

Phương pháp giải:

Để nhân hai đơn thức, ta nhân các hệ số với nhau, nhân các lũy thừa cùng biến, rồi nhân các kết quả đó với nhau.

Lời giải chi tiết:

a) \(\left( {4{x^3}} \right).\left( { - 6{x^3}y} \right) = \left[ {4.\left( { - 6} \right)} \right].\left( {{x^3}.{x^3}} \right).y =  - 24{x^6}y\)

b) \(\left( { - 2y} \right).\left( { - 5x{y^2}} \right) = \left[ {\left( { - 2} \right).\left( { - 5} \right)} \right].x.\left( {y.{y^2}} \right) = 10x{y^3}\)

c) \({\left( { - 2a} \right)^3}.{\left( {2ab} \right)^2} =  - 8{a^3}.4{a^2}{b^2} = \left[ {\left( { - 8} \right).4} \right].\left( {{a^3}.{a^2}} \right).{b^2} =  - 32{a^5}{b^2}\)

HĐ3

a) Hình 3a là bản vẽ sơ lược sàn của một căn hộ (các kích thước tính theo m). Tính diện tích sàn này bằng những cách khác nhau.

b) Nếu vẽ cả ban công thì được sơ đồ như Hình 3b. Hãy tính tổng diện tích của sàn bao gồm cả ban công.

Phương pháp giải:

Sử dụng tính chất phân phối của phép nhân đối với phép cộng, tính chất giao hoán và kết hợp của phép nhân.

Lời giải chi tiết:

a) Cách 1: Diện tích sàn là: \(2x.\left( {y + 3x + 2} \right) = 2x.y + 2x.3x + 2x.2 = 2xy + 6{x^2} + 4x\)

Cách 2: Diện tích sàn là: \(2x.y + 2x.3x + 2x.2 = 2xy + 6{x^2} + 4x\)

b) Diện tích ban công là: \(1.\left( {y + 3x + 2} \right) = y + 3x + 2\)

Tổng diện tích sàn bao gồm cả ban công là: \(\left( {2xy + 6{x^2} + 4x} \right) + \left( {y + 3x + 2} \right) = 2xy + 6{x^2} + 4x + y + 3x + 2 = 2xy + 6{x^2} + y + 7x + 2\)

TH 3

Thực hiện các phép nhân:

a) \(\left( { - 5{a^4}} \right)\left( {{a^2}b - a{b^2}} \right)\)                                             

b) \(\left( {x + 2y} \right)\left( {x{y^2} - 2{y^3}} \right)\)

Phương pháp giải:

- Để nhân đơn thức với đa thức, ta nhân đơn thức đó với từng hạng tử của đa thức rồi cộng các kết quả với nhau.

-  Để nhân hai đa thức, ta nhân từng hạng tử của đa thức này với đa thức kia, rồi cộng các kết quả với nhau

Lời giải chi tiết:

a) \[\left( { - 5{a^4}} \right)\left( {{a^2}b - a{b^2}} \right) =  - 5{a^4}.{a^2}b + 5{a^4}.a{b^2} =  - 5{a^6}b + 5{a^5}{b^2}\]

b) \(\left( {x + 2y} \right)\left( {x{y^2} - 2{y^3}} \right) = x.x{y^2} - x.2{y^3} + 2y.x{y^2} - 2y.2{y^3} = {x^2}{y^2} - 2x{y^3} + 2x{y^3} - 4{y^4} = {x^2}{y^2} - 4{y^4}\)

VD 1

Viết biểu thức tính khoảng cách giữa hai phương tiện trong tình hướng ở câu hỏi mở đầu:

Trên một đoạn sông thẳng, xuất phát cùng lúc từ một bến thuyền, thuyền đi xuôi dòng với tốc độ \(\left( {v + 3} \right)\)km/h, ca nô đi ngược dòng với tốc độ \(\left( {2v - 3} \right)\)km/h. Làm thế nào để tìm được quãng đường của mỗi phương tiện và khoảng cách giữa chúng sau khoảng thời gian \(t\) giờ kể từ khi rời bến?

Phương pháp giải:

Quãng đường = vận tốc . thời gian.

Lời giải chi tiết:

Quãng đường thuyền đi xuôi dòng đi được trong khoảng thời gian \(t\) là:

\(\left( {v + 3} \right)t = vt + 3t\) (km)

Quãng đường ca nô đi ngược dòng đi được trong khoảng thời gian \(t\) là:

\(\left( {2v - 3} \right)t = 2vt - 3t\) (km)

Tổng độ dài quãng đường thuyền và ca nô đi được trong khoảng thời gian \(t\) là:

\(\left( {vt + 3t} \right) + \left( {2vt - 3t} \right) = 3vt\) (km)

Gọi khoảng cách lúc đầu giữa hai phương tiện là \(s\) (km).

Khoảng cách giữa hai phương tiện sau khoảng thời gian \(t\) là:

\(s - 3vt\) (km)

VD 2

Tính diện tích phần tô màu trong Hình 4.

Phương pháp giải:

Áp dụng công thức tính diện tích hình chữ nhật.

Áp dụng qui tắc nhân đa thức, trừ đa thức.

Lời giải chi tiết:

Diện tích hình chữ nhật lớn là: \(5y.\left( {2x + 3y} \right) = 5y.2x + 5y.3y = 10xy + 15{y^2}\)

Diện tích hình chữ nhật nhỏ là: \(x.\left( {x + y} \right) = x.x + x.y = {x^2} + xy\)

Diện tích phần tô màu trong hình 4 là:

\(\left( {10xy + 15{y^2}} \right) - \left( {{x^2} + xy} \right) = 10xy + 15{y^2} - {x^2} - xy = \left( {10xy - xy} \right) + 15{y^2} - {x^2} = 9xy + 15{y^2} - {x^2}\)