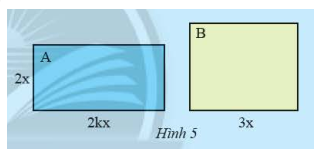
Giải mục 3 trang 15, 16 SGK Toán 8 tập 1– Chân trời sáng tạo

HĐ4

Hình chữ nhật $A$ có chiều rộng $2x$ (cm), chiều dài gấp $k$ ($k > 1$ lần chiều rộng. Hình chữ nhật $B$ có chiều dài $3x$ (cm). Muốn hai hình chữ nhật này có diện tích bằng nhau thì $B$ phải có chiều rộng bằng bao nhiêu?

Phương pháp giải:

Áp dụng công thức tính diện tích hình chữ nhật.

Áp dụng quy tắc nhân đơn thức với đơn thức, chia đơn thức cho đơn thức.

Lời giải chi tiết:

Diện tích hình chữ nhật $A$ là: $2kx.2x = 4k{x^2}$ $c{m^2}$

Muốn hai hình chữ nhật $A$ và $B$ có diện tích bằng nhau thì chiều rộng hình chữ nhật $B$ là:

$4k{x^2}:\left( {3x} \right) = \left( {4:3} \right).\left( {{x^2}:x} \right).k = \frac{4}{3}xk$ (cm)

Thực hành 4

Thực hiện phép chia $8{x^4}{y^5}{z^3}$ cho $2{x^3}{y^4}z$.

Phương pháp giải:

Áp dụng quy tắc chia đơn thức cho đơn thức.

Lời giải chi tiết:

$8{x^4}{y^5}{z^3}:\left( {2{x^3}{y^4}z} \right) = \left( {8:2} \right).\left( {{x^4}:{x^3}} \right).\left( {{y^5}:{y^4}} \right).\left( {{z^3}:z} \right) = 4xy{z^2}$

Vận dụng 3

Tính diện tích đáy của hình hộp chữ nhật có thể tích $V = 12{x^2}y$ và chiều cao bằng $3y$.

Phương pháp giải:

Áp dụng quy tắc chia đơn thức cho đơn thức.

Áp dụng công thức tính diện tích đáy: $S = V:h$ trong đó $S$, $V$, $h$ lần lượt là diện tích đáy, thể tích, chiều cao của hình hộp chữ nhật.

Lời giải chi tiết:

Diện tích đáy của hình hộp chữ nhật là: $12{x^2}y:\left( {3y} \right) = \left( {12:3} \right).\left( {y:y} \right).{x^2} = 4{x^2}$

HĐ5

Một bức tường được trang trí bởi hai tấm giấy dán có cùng chiều cao $2x$ (m) và có diện tích lần lượt là $2{x^2}$ (${m^2}$) và $5xy$ (${m^2}$).

a) Tính chiều rộng của mỗi tấm giấy, từ đó tìm chiều rộng của bức tường.

b) Từ kết quả trên, có thể biết được kết quả của phép chia đa thức $A = 2{x^2} + 5xy$ cho đơn thức $B = 2x$ không? Hãy giải thích.

Phương pháp giải:

Áp dụng quy tắc chia đơn thức cho đơn thức.

Lời giải chi tiết:

a) Chiều rộng của tấm giấy thứ nhất là: $2{x^2}:\left( {2x} \right) = \left( {2:2} \right).\left( {{x^2}:x} \right) = x$ (m)

Chiều rộng tấm giấy thứ hai là: $5xy:\left( {2x} \right) = \left( {5:2} \right).\left( {x:x} \right).y = \frac{5}{2}y$ (m)

Chiều rộng của bức tường là: $x + \frac{5}{2}y$ (m)

b) Kết quả của phép chia đa thức $A = 2{x^2} + 5xy$ cho đa thức $B = 2x$ là $x + \frac{5}{2}y$

Vì $\left( {x + \frac{5}{2}y} \right).\left( {2x} \right) = x.2x + \frac{5}{2}y.2x = 2{x^2} + 5xy$

Thực hành 5

Thực hiện các phép chia:

a) $\left( {5ab - 2{a^2}} \right):a$                                      

b) $\left( {6{x^2}{y^2} - x{y^2} + 3{x^2}y} \right): - 3xy$

Phương pháp giải:

Áp dụng quy tắc chia đa thức cho đơn thức.

Lời giải chi tiết:

a) $\left( {5ab - 2{a^2}} \right):a$

$= \left( {5ab:a} \right) - \left( {2{a^2}:a} \right)$

$= 5b - 2a$

b) $\left( {6{x^2}{y^2} - x{y^2} + 3{x^2}y} \right): - 3xy$

$= \left[ {6{x^2}{y^2}:\left( { - 3xy} \right)} \right] - \left[ {x{y^2}:\left( { - 3xy} \right)} \right] + \left[ {3{x^2}y:\left( { - 3xy} \right)} \right]$

$=  - 2xy - \left( { - \frac{1}{3}y} \right) + \left( { - x} \right)$

$=  - 2xy + \frac{1}{3}y - x$

Vận dụng 4

Tính chiều cao của hình hộp chữ nhật có thể tích $V = 6{x^2}y - 8x{y^2}$ và diện tích đáy $S = 2xy$.

Phương pháp giải:

Áp dụng công thức tính chiều cao hình hộp chữ nhật: $h = V:S$ trong đó $S$, $V$, $h$ lần lượt là diện tích đáy, thể tích, chiều cao của hình hộp chữ nhật.

Áp dụng quy tắc chia đa thức cho đơn thức.

Lời giải chi tiết:

Chiều cao của hình hộp chữ nhật là:

$\left( {6{x^2}y - 8x{y^2}} \right):\left( {2xy} \right) = \left[ {6{x^2}y:\left( {2xy} \right)} \right] - \left[ {8x{y^2}:\left( {2xy} \right)} \right]$$= 3x - 4y$