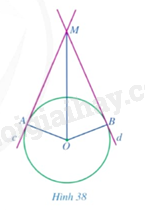
Giải mục 2 trang 108, 109 SGK Toán 9 tập 1 - Cánh diềuCho đường tròn (left( {O;R} right)). Các đường thẳng (c,d) lần lượt tiếp xúc với đường tròn (left( {O;R} right)) tại (A,B) và cắt nhau tại (M) (Hình 38). a) Các tam giác (MOA) và (MOB) có bằng nhau hay không? b) Hai đoạn thẳng (MA) và (MB) có bằng nhau hay không? c) Tia (MO) có phải là tia phân giác của góc (AMB) hay không? d) Tia (OM) có phải là tia phân giác của gics (AOB) hay không? Tổng hợp Đề thi vào 10 có đáp án và lời giải Toán - Văn - Anh
Lựa chọn câu để xem lời giải nhanh hơn
HĐ3 Video hướng dẫn giải Trả lời câu hỏi Hoạt động 3 trang 108 SGK Toán 9 Cánh diều Cho đường tròn (O;R)(O;R). Các đường thẳng c,dc,d lần lượt tiếp xúc với đường tròn (O;R)(O;R) tại A,BA,B và cắt nhau tại MM (Hình 38).
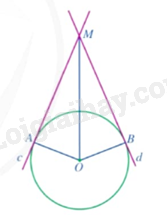
a) Các tam giác MOAMOA và MOBMOB có bằng nhau hay không? b) Hai đoạn thẳng MAMA và MBMB có bằng nhau hay không? c) Tia MOMO có phải là tia phân giác của góc AMBAMB hay không? d) Tia OMOM có phải là tia phân giác của góc AOBAOB hay không? Phương pháp giải: Dựa vào tam giác bằng nhau để chứng minh. Lời giải chi tiết: a) Do MAMA là tiếp tuyến của (O;R)(O;R) nên MA⊥AOMA⊥AO suy ra ^MAO=90∘ˆMAO=90∘. Do MBMB là tiếp tuyến của (O;R)(O;R) nên MB⊥BOMB⊥BO suy ra ^MBO=90∘ˆMBO=90∘. Xét tam giác MOAMOAvà tam giác MOBMOB có: ^MAO=^MBO=90∘ˆMAO=ˆMBO=90∘ OA=OB=ROA=OB=R OMOM chung ⇒ΔMOA=ΔMOB⇒ΔMOA=ΔMOB (cạnh huyền – cạnh góc vuông). b) Do ΔMOA=ΔMOBΔMOA=ΔMOB nên MA=MBMA=MB (2 cạnh tương ứng). c) Do ΔMOA=ΔMOBΔMOA=ΔMOB nên ^AMO=^BMOˆAMO=ˆBMO (2 góc tương ứng) suy ra MOMO là tia phân giác của góc AMBAMB. d) Do ΔMOA=ΔMOBΔMOA=ΔMOB nên ^MOA=^MOBˆMOA=ˆMOB (2 góc tương ứng) suy ra OMOM là tia phân giác của góc AOBAOB. LT4 Video hướng dẫn giải Trả lời câu hỏi Luyện tập 4 trang 109 SGK Toán 9 Cánh diều Cho đường tròn (O;R)(O;R) và điểm MM nằm ngoài đường tròn. Hai đường thẳng c,dc,d qua MM lần lượt tiếp xúc với (O)(O) tại A,BA,B biết ^AMB=120∘ˆAMB=120∘. Chứng minh AB=RAB=R. Phương pháp giải: Dựa vào tính chất 2 tiếp tuyến cắt nhau và tỉ số lượng giác để làm bài toán. Lời giải chi tiết:
Cách 1. Vì MA,MBMA,MB là các tiếp tuyến của (O)(O) nên MO là tia phân giác của góc AMB, suy ra ^AMO=^BMO=^AMB2=60∘ˆAMO=ˆBMO=ˆAMB2=60∘. Xét tam giác AMOAMO vuông tại AA có: ^AMO+^MOA=9060∘+^MOA=90∘^MOA=30∘ Vì MA,MB là các tiếp tuyến của (O) nên OM là tia phân giác của góc AOB, suy ra ^AOB=2^AOM=2.30∘=60∘. Xét tam giác AOB có: OA=OB=R nên tam giác AOB cân tại O. Lại có ^AOB=60∘ suy ra tam giác AOB là tam giác đều. Vậy AO=OB=AB=R. Cách 2. Vì MA, MB là tiếp tuyến của (O) nên MA⊥OA, MB⊥OB suy ra ^MAO=^MBO=90∘ Xét tứ giác OAMB có: ^AMB+^MAO+^MBO+^AOB=360∘ Suy ra ˆO=360∘−120∘−90∘−90∘=60∘ Xét ΔOAB có OA=OB=R suy ra ΔOAB cân tại O Lại có ˆO=60∘ (cmt) Suy ra ΔOAB đều Do đó OA=OB=AB=R (đpcm)
>> Học trực tuyến Lớp 10 cùng thầy cô giáo giỏi tại Tuyensinh247.com, (Xem ngay) Cam kết giúp học sinh học tốt, bứt phá điểm 9,10 chỉ sau 3 tháng, làm quen kiến thức, định hướng luyện thi TN THPT, ĐGNL, ĐGTD ngay từ lớp 10
|