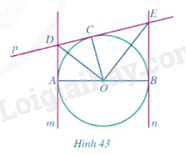
Giải bài tập 5 trang 110 SGK Toán 9 tập 1 - Cánh diềuCho đường tròn (left( {O;R} right)) đường kính (AB) và các đường thẳng (m,n,p) lần lượt tiếp xúc với đường tròn tại (A,B,C) (Hình 43). Chứng minh: a) (AD + BE = DE); b) (widehat {COD} = frac{1}{2}widehat {COA}) và (widehat {COE} = frac{1}{2}widehat {COB}); c) Tam giác (ODE) vuông; d) (frac{{OD.OE}}{{DE}} = R). Tổng hợp Đề thi vào 10 có đáp án và lời giải Toán - Văn - Anh Đề bài Cho đường tròn (O;R) đường kính AB và các đường thẳng m,n,p lần lượt tiếp xúc với đường tròn tại A,B,C (Hình 43).
Chứng minh: a) AD+BE=DE; b) ^COD=12^COA và ^COE=12^COB; c) Tam giác ODE vuông; d) OD.OEDE=R. Video hướng dẫn giải Phương pháp giải - Xem chi tiết Dựa vào tính chất tiếp tuyến để chứng minh. Lời giải chi tiết a) Do DC,DA cùng là tiếp tuyến của đường tròn (O) nên DA=DC. Do EC,EB cùng là tiếp tuyến của đường tròn (O) nên CE=BE. Lại có: DC+CE=DE suy ra DA+EB=DE. b) Do DC,DA cùng là tiếp tuyến của đường tròn (O) nên OD là tia phân giác của góc COA. Suy ra ^COD=12^COA. Do EC,EB cùng là tiếp tuyến của đường tròn (O) nên OE là tia phân giác của góc COB. Suy ra ^COE=12^COB. c) Ta có: ^COA+^COB=180∘ (hai góc kề bù). Suy ra 12(^COA+^COB)=12.180∘=90∘ Do đó 12^COA+12^COB=90∘. Mà ^COD=12^COA,^COE=12^COB nên ^COD+^COE=90∘ hay ^DOE=90∘. Vậy tam giác ODE vuông tại O. d) Vì DE là tiếp tuyến của (O) nên DE⊥CO Suy ra ^DCO=90∘ Xét ΔODE và ΔCDO có: ^DOE=^DCO=90∘ ^ODE (góc chung) suy ra ΔODE∽ΔCDO (g.g) Do đó OEOC=DEOD Dẫn đến OE⋅OD=DE⋅OC Suy ra OD.OEDE=OC. hay OD.OEDE=R. (đpcm)  Chia sẻ Bình luận
Tham Gia Group 2K10 Ôn Thi Vào Lớp 10 Miễn Phí
>> Học trực tuyến Lớp 10 cùng thầy cô giáo giỏi tại Tuyensinh247.com, (Xem ngay) Cam kết giúp học sinh học tốt, bứt phá điểm 9,10 chỉ sau 3 tháng, làm quen kiến thức, định hướng luyện thi TN THPT, ĐGNL, ĐGTD ngay từ lớp 10
|
