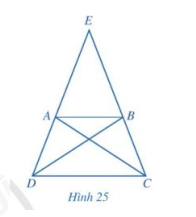
Giải mục 2 trang 102 SGK Toán 8 tập 1 - Cánh diều

HĐ3

Cho hình thang cân ABCD có AB // CD , AB < CD, E là giao điểm của AD và BC (Hình 25)

 

a) So sánh các cặp góc: \(\widehat {E{\rm{D}}C}\) và \(\widehat {EC{\rm{D}}}\); \(\widehat {E{\rm{A}}B}\) và \(\widehat {EBA}\).

b) So sánh các cặp đoạn thẳng: EA và EB, ED và EC. Từ đó, hãy so sánh AD và BC.

c) Hai tam giác ADC và BCD có bằng nhau hay không? Từ đó, hãy so sánh AC và BD

Phương pháp giải:

Quan sát hình 25.

Lời giải chi tiết:

a, Do ABCD là hình thang cân nên.

\(\widehat {ADC} = \widehat {BCD}\)hay \(\widehat {EDC} = \widehat {ECD}\)

Do ABCD là hình thang cân nên

\(\widehat {BAD} = \widehat {ABC}\left( 1 \right)\)

Mà:

\(\begin{array}{l}\widehat {BAD} + \widehat {EAB} = {180^0}\\\widehat {ABC} + \widehat {EBA} = {180^0}\end{array}\)

Suy ra:

\(\begin{array}{l}\widehat {BAD} + \widehat {EAB} = \widehat {ABC} + \widehat {EBC}\\ \Rightarrow \widehat {EAB} = \widehat {EBA}\end{array}\)(do(1))

b, Do \(\widehat {EAB} = \widehat {EBA}\) suy ra \(\Delta EAB\)cân tại E nên EA = EB

Do \(\widehat {EDC} = \widehat {ECD}\) suy ra \(\Delta ECD\)cân tại E nên ED = EC

Mà: ED = EC

Suy ra EA + AD = EB + BC

Suy ra AD = BC (do EA = EB)

c, Xét \(\Delta ADC\) và \(\Delta BCD\) có:

AD = BC

\(\widehat {ADC} = \widehat {BCD}\)

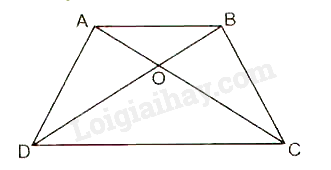
DC chung

Suy ra: \(\Delta ADC = \Delta BCD(c.g.c) \Rightarrow AC = BD\)

LT1

Cho hình thang cân, ABCD có AB //CD. Chứng minh \(\widehat {A{\rm{DB}}} = \widehat {BCA}\)

Phương pháp giải:

Chứng minh \(\Delta ADB = \Delta BCA(c.g.c)\)

Lời giải chi tiết:

Do tứ giác ABCD là hình thang cân nên

AD = BC.

AC = BD.

Xét \(\Delta ADB\) và \(\Delta BCA\) có:

AB chung, AD = BC, AC = BD

\(\Rightarrow \Delta ADB=\Delta BCA\) (c.c.c)