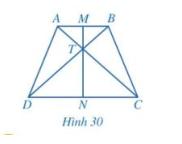
Giải bài 1 trang 103 SGK Toán 8 tập 1 - Cánh diều

Đề bài

Cho hình thang cân ABCD có AB // CD, AB < CD. Gọi M, N lần lượt là trung điểm của cạnh AB, CD và T là giao điểm của AC và BD (hình 30)

 

a) $\widehat {TA{\rm{D}}} = \widehat {TBC},\widehat {T{\rm{D}}A} = \widehat {TCB}$

b) $TA = TB,T{\rm{D}} = TC$

c) MN là đường trung trực của cả hai đoạn thẳng AB và CD

Lời giải chi tiết

a, Xét $\Delta ADC$và $\Delta BDC$có:

DC là cạnh chung.

$\widehat {ADC} = \widehat {BCD}$(do ABCD là hình thang cân)

AD = BC

$\Rightarrow \Delta ADC = \Delta BDC(c.g.c)$

$\Rightarrow \widehat {CAD} = \widehat {DBC}$(2 góc tương ứng) hay

Do: $\Delta ADC = \Delta BDC$

Xét $\Delta BAD$và $\Delta ACB$có:

AB chung

AD = BC

AC = BD

$\Rightarrow \Delta BDA = \Delta ACB$ (c.c.c)

$\Rightarrow \widehat {BDA} = \widehat {ACB}$(2 góc tương ứng) hay $\widehat {TDA} = \widehat {TCB}$

b, Xét $\Delta TAD$và $\Delta TBC$có:

$\widehat {TAD} = \widehat {TBC}$(theo câu a)

AD = BC (ABCD là hình thang cân)

$\widehat {TDA} = \widehat {TCB}$(theo câu a)

$\Rightarrow \Delta TAD = \Delta TBC \Rightarrow TA = TB,TC = TD$

c, Vì: TA = TB $\Rightarrow \Delta ATB$cân tại T suy ra TM là trung trực của AB

TC = TD $\Rightarrow \Delta DTC$cân tại T suy ra TN là trung trực của CD

Mà: M, T, N thẳng hàng. Nên MN là đường trung trực của cả 2 đường thẳng AB và CD