Giải mục 1 trang 62, 63 SGK Toán 8 - Cùng khám pháGiải thích vì sao trong Hình 6.76, \(\Delta A'B'C'\) đồng dạng với \(\Delta ABC\)?
Lựa chọn câu để xem lời giải nhanh hơn
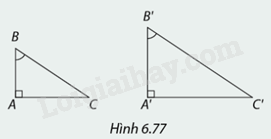
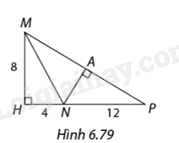
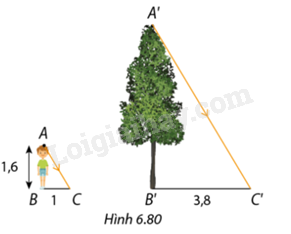
Hoạt động 1 Giải thích vì sao trong Hình 6.76, \(\Delta A'B'C'\) đồng dạng với \(\Delta ABC\)? Phương pháp giải: Áp dụng trường hợp đồng dạng cạnh-góc-cạnh của tam giác để giải thích Lời giải chi tiết: Xét tam giác \(ABC\) và tam giác \(A'B'C'\), có: \(\widehat A = \widehat {A'} = 90^\circ \) \(\frac{{AB}}{{A'B'}} = \frac{{AC}}{{A'C'}} = \frac{1}{2}\) => \(\Delta ABC\)∽\(\Delta A'B'C'\) Hoạt động 2 Giải thích vì sao trong Hình 6.77, \(\Delta A'B'C'\) đồng dạng với \(\Delta ABC\)? Phương pháp giải: Áp dụng trường hợp đồng dạng góc-góc để giải thích Lời giải chi tiết: Xét tam giác \(ABC\) và tam giác \(A'B'C'\), có: \(\begin{array}{l}\widehat A = \widehat {A'} = 90^\circ \\\widehat B = \widehat {B'}\left( {gt} \right)\end{array}\) => \(\Delta ABC\)∽\(\Delta A'B'C'\) Luyện tập 1 Chứng minh rằng trong Hình 6.79, \(\Delta HMN\) đồng dạng với \(\Delta HPM\) và \(\Delta APN\). Phương pháp giải: Nếu một góc nhọn của tam giác vuông này bằng một góc nhọn của tam giác vuông kia thì hai tam giác vuông đó đồng dạng. Nếu hai cạnh góc vuông của tam giác vuông này tỉ lệ với hai cạnh góc vuông của tam giác vuông kia thì hai tam giác vuông đó đồng dạng. Lời giải chi tiết: Xét hai tam giác vuông \(HMN\) và \(HPM\), ta có: \(\frac{{HM}}{{HP}} = \frac{{HN}}{{HM}} = \frac{1}{2}\) \(\widehat H\) chung => \(\Delta HMN\)∽\(\Delta HPM\) Xét hai tam giác vuông \(HMN\) và \(APN\), ta có: \(\widehat H = \widehat {NAP} = 90^\circ \) \(\widehat {HMN} = \widehat {APN}\) (do \(\Delta HMN\)∽\(\Delta HPM\)) => \(\Delta HMN\)∽\(\Delta APN\) (cạnh huyền-góc nhọn) Vận dụng 1 Vào một thời điểm trong ngày, bóng của bạn An trên mặt đất là \(BC = 1m\), còn bóng cây \(A'B'\) là \(B'C' = 3,8m\) (Hình 6.80). Biết An cao 1,6m, hỏi cây cao bao nhiêu mét? Làm tròn kết quả đến hàng phần mười. Phương pháp giải: Nếu một góc nhọn của tam giác vuông này bằng một góc nhọn của tam giác vuông kia thì hai tam giác vuông đó đồng dạng. Nếu hai cạnh góc vuông của tam giác vuông này tỉ lệ với hai cạnh góc vuông của tam giác vuông kia thì hai tam giác vuông đó đồng dạng. Lời giải chi tiết: Ta có: \(\Delta ABC\)∽\(\Delta A'B'C'\), nên suy ra tỉ số đồng dạng: \(\begin{array}{l}\frac{{AB}}{{A'B'}} = \frac{{BC}}{{B'C'}}\\ \Leftrightarrow \frac{{1,6}}{{A'B'}} = \frac{1}{{3,8}}\\ \Rightarrow A'B' = 6,08\end{array}\) Vậy cây cao 6,08 m.
|