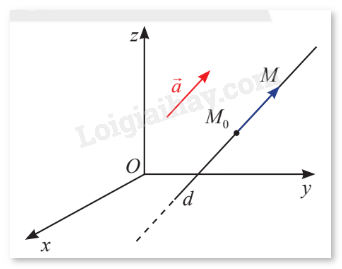
Giải mục 1 trang 44, 45, 46, 47 SGK Toán 12 tập 2 - Chân trời sáng tạoTrong không gian \(Oxyz\), cho điểm \({M_0}\) cố định và vectơ \(\vec a\) khác \(\vec 0\). Có bao nhiêu đường thẳng \(d\) đi qua \({M_0}\) và song song hoặc trùng với giá của \(\vec a\)? Tổng hợp đề thi học kì 1 lớp 12 tất cả các môn - Chân trời sáng tạo Toán - Văn - Anh - Lí - Hóa - Sinh - Sử - Địa
Lựa chọn câu để xem lời giải nhanh hơn
HĐ1 Trả lời câu hỏi Hoạt động 1 trang 44 SGK Toán 12 Chân trời sáng tạo Trong không gian \(Oxyz\), cho điểm \({M_0}\) cố định và vectơ \(\vec a\) khác \(\vec 0\). Có bao nhiêu đường thẳng \(d\) đi qua \({M_0}\) và song song hoặc trùng với giá của \(\vec a\)?
Phương pháp giải: Trong không gian, qua một điểm không nằm trên một đường thẳng, có duy nhất một đường thẳng đi qua điểm và song song với đường thẳng đó. Lời giải chi tiết: Nếu điểm \({M_0}\) nằm trên giá của vectơ \(\vec a\), thì đường thẳng đó là đường thẳng duy nhất cần tìm. Nếu điểm \({M_0}\) không nằm trên giá của vectơ \(\vec a\), do trong không gian, qua một điểm không nằm trên một đường thẳng, có duy nhất một đường thẳng đi qua điểm và song song với đường thẳng đó, nên tồn tại duy nhất một đường thẳng đi qua \({M_0}\) và song song với giá của vectơ \(\vec a\). Như vậy, có duy nhất một đường thẳng \(d\) đi qua \({M_0}\) và song song hoặc trùng với giá của \(\vec a.\) TH1 Trả lời câu hỏi Thực hành 1 trang 44 SGK Toán 12 Chân trời sáng tạo Trong không gian \(Oxyz\), cho hình lăng trụ tam giác \(ABC.A'B'C'\) với \(A\left( {1;2;1} \right)\), \(B\left( {7;5;3} \right)\), \(C\left( {4;2;0} \right)\), \(A'\left( {4;9;9} \right)\). Tìm toạ độ một vectơ chỉ phương của mỗi đường thẳng \(AB\), \(A'C'\) và \(BB'.\)
Phương pháp giải: Các đường thẳng \(AB\), \(A'C'\) và \(BB'\) có một vectơ chỉ phương lần lượt là \(\overrightarrow {AB} \), \(\overrightarrow {AC} \) và \(\overrightarrow {AA'} .\) Lời giải chi tiết: Ta có \(\overrightarrow {AB} \left( {6;3;2} \right)\) là một vectơ chỉ phương của đường thẳng \(AB.\) Ta có \(AC\parallel A'C'\) nên \(\overrightarrow {AC} \left( {3;0; - 1} \right)\) là một vectơ chỉ phương của đường thẳng \(A'C'.\) Ta có \(AA'\parallel BB'\) nên \(\overrightarrow {AA'} \left( {3;7;8} \right)\) là một vectơ chỉ phương của đường thẳng \(BB'.\) HĐ2 Trả lời câu hỏi Hoạt động 2 trang 44 SGK Toán 12 Chân trời sáng tạo Trong không gian \(Oxyz\), cho đường thẳng \(d\) đi qua điểm \({M_0}\left( {{x_0};{y_0};{z_0}} \right)\) cố định và có vectơ chỉ phương là \(\vec a = \left( {{a_1};{a_2};{a_3}} \right)\) khác \(\vec 0.\) a) Giải thích tại sao ta có thể viết \(M \in d \Leftrightarrow \overrightarrow {{M_0}M} = t\vec a{\rm{ }}\left( {t \in \mathbb{R}} \right).\) b) Với \(M\left( {x;y;z} \right)\) thuộc \(d\), hãy tính \(x\), \(y\), \(z\) theo \({x_0}\), \({y_0}\), \({z_0}\) và \({a_1}\), \({a_2}\), \({a_3}.\)
Phương pháp giải: a) Chỉ ra rằng \(\overrightarrow {{M_0}M} \) và \(\vec a\) là hai vectơ cùng phương. b) Sử dụng tính chất của hai vectơ cùng phương. Lời giải chi tiết: a) Ta có \(\vec a\) là vectơ chỉ phương của đường thẳng \(d\). Nếu \(M \in d\), ta có \(d\) đi qua hai điểm \(M\) và \({M_0}\) nên hai vectơ \(\overrightarrow {{M_0}M} \) và \(\vec a\) là hai vectơ cùng phương, suy ra \(\overrightarrow {{M_0}M} = t\vec a\) với \(t \in \mathbb{R}\). Ngược lại, với \(\overrightarrow {{M_0}M} = t\vec a\) thì \(\overrightarrow {{M_0}M} \) và \(\vec a\) là hai vectơ cùng phương. Mà \(\vec a\) là vectơ chỉ phương của đường thẳng \(d\), nên \(\overrightarrow {{M_0}M} \) cũng là một vectơ chỉ phương của đường thẳng \(d\). Do \({M_0} \in d\), nên ta suy ra \(M \in d\). b) Ta có \(\overrightarrow {{M_0}M} = \left( {x - {x_0};y - {y_0};z - {z_0}} \right)\) và \(\vec a = \left( {{a_1};{a_2};{a_3}} \right)\). Theo câu a, ta có \(\overrightarrow {{M_0}M} = t\vec a\) nên \(\left( {x - {x_0};y - {y_0};z - {z_0}} \right) = t\left( {{a_1};{a_2};{a_3}} \right)\) Suy ra \(\left\{ \begin{array}{l}x - {x_0} = t{a_1}\\y - {y_0} = t{a_2}\\z - {z_0} = t{a_3}\end{array} \right.\) hay \(\left\{ \begin{array}{l}x = {x_0} + t{a_1}\\y = {y_0} + t{a_2}\\z = {z_0} + t{a_3}\end{array} \right.\) TH2 Trả lời câu hỏi Thực hành 2 trang 46 SGK Toán 12 Chân trời sáng tạo Cho đường thẳng \(d\) có phương trình tham số \(\left\{ \begin{array}{l}x = - 1 + 8t\\y = - 4t\\z = 3 + 12t\end{array} \right.\) a) Tìm hai vectơ chỉ phương của \(d.\) b) Tìm ba điểm trên \(d.\) Phương pháp giải: a) Từ phương trình tham số, chỉ ra hai vectơ chỉ phương của đường thẳng. b) Từ phương trình tham số, chỉ ra ba điểm nằm trên đường thẳng. Lời giải chi tiết: a) Từ phương trình tham số, ta có \(\vec a = \left( {8; - 4;12} \right)\) là một vectơ chỉ phương của đường thẳng \(d.\) Chọn \(\vec b = \frac{1}{4}\vec a = \left( {2; - 1;3} \right)\), ta có \(\vec b\) cũng là một vectơ chỉ phương của đường thẳng \(d.\) b) Thay \(t = 0\) vào phương trình tham số của \(d\), ta được \(\left\{ \begin{array}{l}x = - 1 + 8.0\\y = - 4.0\\z = 3 + 12.0\end{array} \right.\) hay \(\left\{ \begin{array}{l}x = - 1\\y = 0\\z = 3\end{array} \right.\) Vậy \(A\left( { - 1;0;3} \right)\) là một điểm nằm trên đường thẳng \(d.\) Thay \(t = 1\) vào phương trình tham số của \(d\), ta được \(\left\{ \begin{array}{l}x = - 1 + 8.1\\y = - 4.1\\z = 3 + 12.1\end{array} \right.\) hay \(\left\{ \begin{array}{l}x = 7\\y = - 4\\z = 15\end{array} \right.\) Vậy \(B\left( {7; - 4;15} \right)\) là một điểm nằm trên đường thẳng \(d.\) Thay \(t = 2\) vào phương trình tham số của \(d\), ta được \(\left\{ \begin{array}{l}x = - 1 + 8.2\\y = - 4.2\\z = 3 + 12.2\end{array} \right.\) hay \(\left\{ \begin{array}{l}x = 15\\y = - 8\\z = 27\end{array} \right.\) Vậy \(C\left( {15; - 8;27} \right)\) là một điểm nằm trên đường thẳng \(d.\) TH3 Trả lời câu hỏi Thực hành 3 trang 46 SGK Toán 12 Chân trời sáng tạo Viết phương trình tham số của đường thẳng \(d\) đi qua điểm \(A\left( {5;0; - 7} \right)\) và nhận \(\vec v = \left( {9;0; - 2} \right)\) làm vectơ chỉ phương. Đường thẳng \(d\) có đi qua điểm \(M\left( { - 4;0; - 5} \right)\) không? Phương pháp giải: Viết phương trình đường thẳng \(d.\) Để kiểm tra điểm \(M\) có nằm trên đường thẳng \(d\) hay không, thực hiện thay hoành độ của điểm \(M\) vào phương trình để tìm tham số \(t\), sau đó thay tung độ và cao độ của \(z\) vào các phương trình còn lại để kiểm tra xem phương trình có thoả mãn hay không. Lời giải chi tiết: Phương trình tham số của \(d\) là \(\left\{ \begin{array}{l}x = 5 + 9t\\y = 0\\z = - 7 - 2t\end{array} \right.\) Thay hoành độ điểm \(M\) vào phương trình \(x = 5 + 9t\), ta được \( - 4 = 5 + 9t\), suy ra \(t = - 1.\) Thay \(t = - 1\), tung độ và cao độ của điểm \(M\) vào các phương trình còn lại, ta thấy các phương trình đó thoả mãn (do \(0 = 0\) và \( - 5 = - 7 - 2.\left( { - 1} \right)\)). Vậy đường thẳng \(d\) đi qua điểm \(M.\) HĐ3 Trả lời câu hỏi Hoạt động 3 trang 46 SGK Toán 12 Chân trời sáng tạo Cho đường thẳng \(d\) có phương trình tham số \(\left\{ \begin{array}{l}x = {x_0} + {a_1}t\\y = {y_0} + {a_2}t\\z = {z_0} + {a_3}t\end{array} \right.\) với \({a_1}\), \({a_2}\), \({a_3}\) đều khác 0. Lấy điểm \(M\left( {x;y;z} \right)\) bất kì thuộc \(d\). So sánh các biểu thức \(\frac{{x - {x_0}}}{{{a_1}}}\); \(\frac{{y - {y_0}}}{{{a_2}}}\); \(\frac{{z - {z_0}}}{{{a_3}}}.\) Phương pháp giải: Lần lượt tính các biểu thức \(\frac{{x - {x_0}}}{{{a_1}}}\); \(\frac{{y - {y_0}}}{{{a_2}}}\); \(\frac{{z - {z_0}}}{{{a_3}}}\) và so sánh các kết quả. Lời giải chi tiết: Ta có \(M\left( {x;y;z} \right)\) thuộc \(d\), nên ta có \(\left\{ \begin{array}{l}x = {x_0} + {a_1}t\\y = {y_0} + {a_2}t\\z = {z_0} + {a_3}t\end{array} \right.\) Suy ra \(\frac{{x - {x_0}}}{{{a_1}}} = t\); \(\frac{{y - {y_0}}}{{{a_2}}} = t\); \(\frac{{z - {z_0}}}{{{a_3}}} = t.\) Như vậy \(\frac{{x - {x_0}}}{{{a_1}}} = \frac{{y - {y_0}}}{{{a_2}}} = \frac{{z - {z_0}}}{{{a_3}}}.\) TH4 Trả lời câu hỏi Thực hành 4 trang 46 SGK Toán 12 Chân trời sáng tạo Viết phương trình chính tắc của đường thẳng \(d\) đi qua điểm \({M_0}\left( {5;0; - 6} \right)\) và nhận \(\vec a = \left( {3;2; - 4} \right)\) làm vectơ chỉ phương. Phương pháp giải: Phương trình chính tắc của đường thẳng \(d\) đi qua điểm \(M\left( {{x_0};{y_0};{z_0}} \right)\) và nhận \(\vec a = \left( {{a_1};{a_2};{a_3}} \right)\) làm vectơ chỉ phương là \(\frac{{x - {x_0}}}{{{a_1}}} = \frac{{y - {y_0}}}{{{a_2}}} = \frac{{z - {z_0}}}{{{a_3}}}.\) Lời giải chi tiết: Phương trình chính tắc của đường thẳng \(d\) đi qua điểm \({M_0}\left( {5;0; - 6} \right)\) và nhận \(\vec a = \left( {3;2; - 4} \right)\) làm vectơ chỉ phương là \(\frac{{x - 5}}{3} = \frac{{y - 0}}{2} = \frac{{z - \left( { - 6} \right)}}{{ - 4}}\) hay \(\frac{{x - 5}}{3} = \frac{y}{2} = \frac{{z + 6}}{{ - 4}}.\) HĐ4 Trả lời câu hỏi Hoạt động 4 trang 47 SGK Toán 12 Chân trời sáng tạo Cho đường thẳng \(d\) đi qua hai điểm \(A\left( {2;2;1} \right)\) và \(B\left( {4;5;3} \right).\) a) Tìm một vectơ chỉ phương của \(d.\) b) Viết phương trình tham số và phương trình chính tắc của \(d.\) Phương pháp giải: a) Đường thẳng \(d\) đi qua hai điểm \(A\) và \(B\) nên nó nhận \(\overrightarrow {AB} \) là một vectơ chỉ phương. b) Viết phương trình đường thẳng \(d\) đi qua \(A\) và có một vectơ chỉ phương là \(\overrightarrow {AB} .\) Lời giải chi tiết: a) Đường thẳng \(d\) đi qua hai điểm \(A\left( {2;2;1} \right)\) và \(B\left( {4;5;3} \right)\) nên nó nhận \(\overrightarrow {AB} \left( {2;3;2} \right)\) là một vectơ chỉ phương. b) Phương trình tham số của đường thẳng \(d\) đi qua \(A\left( {2;2;1} \right)\) và có một vectơ chỉ phương \(\overrightarrow {AB} \left( {2;3;2} \right)\) là \(\left\{ \begin{array}{l}x = 2 + 2t\\y = 2 + 3t\\z = 1 + 2t\end{array} \right.\) Phương trình chính tắc của đường thẳng \(d\) đi qua \(A\left( {2;2;1} \right)\) và có một vectơ chỉ phương \(\overrightarrow {AB} \left( {2;3;2} \right)\) là \(\frac{{x - 2}}{2} = \frac{{y - 2}}{3} = \frac{{z - 1}}{2}.\) TH5 Trả lời câu hỏi Thực hành 5 trang 47 SGK Toán 12 Chân trời sáng tạo Viết phương trình tham số và phương trình chính tắc của đường thẳng \(MN\), biết \(M\left( {2;0; - 1} \right)\) và \(N\left( {4;3;1} \right).\) Phương pháp giải: Đường thẳng \(MN\) đi qua hai điểm \(M\) và \(N\) nên \(\overrightarrow {MN} \) là một vectơ chỉ phương của đường thẳng, từ đó viết được phương trình tham số và phương trình chính tắc của đường thẳng \(MN.\) Lời giải chi tiết: Ta có \(\overrightarrow {MN} = \left( {2;3;2} \right)\). Đường thẳng \(MN\) đi qua điểm \(M\left( {2;0; - 1} \right)\) và có một vectơ chỉ phương là \(\overrightarrow {MN} = \left( {2;3;2} \right)\) nên phương trình tham số của đường thẳng \(MN\) là \(\left\{ \begin{array}{l}x = 2 + 2t\\y = 0 + 3t\\z = - 1 + 2t\end{array} \right.\) hay \(\left\{ \begin{array}{l}x = 2 + 2t\\y = 3t\\z = - 1 + 2t\end{array} \right.\); phương trình chính tắc của đường thẳng \(MN\) là \(\frac{{x - 2}}{2} = \frac{{y - 0}}{3} = \frac{{z + 1}}{2}\) hay \(\frac{{x - 2}}{2} = \frac{y}{3} = \frac{{z + 1}}{2}.\) VD1 Trả lời câu hỏi Vận dụng 1 trang 47 SGK Toán 12 Chân trời sáng tạo Một mô hình cầu treo được thiết kế trong không gian \(Oxyz\) như hình dưới đây. Viết phương trình tham số của làn đường \(d\) đi qua hai điểm \(M\left( {4;3;20} \right)\) và \(N\left( {4;1000;20} \right).\)
Phương pháp giải: Đường thẳng \(d\) đi qua hai điểm \(M\) và \(N\) nên \(\overrightarrow {MN} \) là một vectơ chỉ phương của đường thẳng, từ đó viết được phương trình tham số của \(d.\) Lời giải chi tiết: Ta có \(\overrightarrow {MN} = \left( {0;997;0} \right)\). Đường thẳng \(d\) đi qua hai điểm \(M\) và \(N\) nên \(\overrightarrow {MN} \) là một vectơ chỉ phương của đường thẳng. Suy ra vectơ \(\vec u = \frac{1}{{997}}\overrightarrow {MN} = \left( {0;1;0} \right)\) cũng là một vectơ chỉ phương của đường thẳng \(d.\) Phương trình tham số của làn đường \(d\) đi qua \(M\left( {4;3;20} \right)\) và có một vectơ chỉ phương \(\vec u = \left( {0;1;0} \right)\) là \(\left\{ \begin{array}{l}x = 4 + 0t\\y = 3 + t\\z = 20 + 0t\end{array} \right.\) hay \(\left\{ \begin{array}{l}x = 4\\y = 3 + t\\z = 20\end{array} \right.\). Đặt \(t' = t + 3\), phương trình tham số của làn đường \(d\) là \(\left\{ \begin{array}{l}x = 4\\y = t'\\z = 20\end{array} \right.\).
|