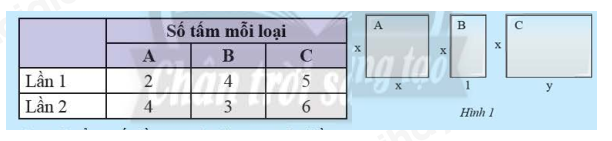
Giải mục 1 trang 12 SGK Toán 8 tập 1– Chân trời sáng tạoTại một công trình xây dựng, người ta dùng ba loại tấm kính chống nắng , và với các kích thước như Hình 1 (tính bằng m). Giá tiền các tấm kính được tính theo diện tích với đơn giá đồng/ . Tại đây có hai lần nhập vật liệu như bảng sau: Tổng hợp đề thi học kì 2 lớp 8 tất cả các môn - Chân trời sáng tạo Toán - Văn - Anh - Khoa học tự nhiên
Lựa chọn câu để xem lời giải nhanh hơn
HĐ1 Video hướng dẫn giải Tại một công trình xây dựng, người ta dùng ba loại tấm kính chống nắng , và với các kích thước như Hình 1 (tính bằng m). Giá tiền các tấm kính được tính theo diện tích với đơn giá đồng/. Tại đây có hai lần nhập vật liệu như bảng sau: a) Tính tổng số tiền mua kính của cả hai lần. b) Số tiền lần 2 nhiều hơn lần 1 bao nhiêu? Phương pháp giải: Sử dụng công thức tính diện tích hình vuông, hình chữ nhật để tính được số tiền mua kính. Lời giải chi tiết: a) Diện tích tấm kính chống nắng là: () Diện tích tấm kính chống nắng là: () Diện tích tấm kính chống nắng là: () Số tiền mua kính lần 1 là: (đồng) Số tiền mua kính lần 2 là: (đồng) Tổng số tiền mua kính cả hai lần là: b) Số tiền lần 2 nhiều hơn lần 1 là:
Thực hành 1 Video hướng dẫn giải Cho hai đa thức và . Tính và . Phương pháp giải: Muốn cộng hay trừ hai đa thức ta làm như sau: - Viết hai đa thức trong ngoặc và nối với nhau bằng dấu cộng hay trừ. - Bỏ dấu ngoặc rồi thu gọn đa thức thu được. Lời giải chi tiết: Ta có:
Ta có:
|