Giải đề thi học kì 2 toán lớp 6 năm 2020 - 2021 trường Archimeches

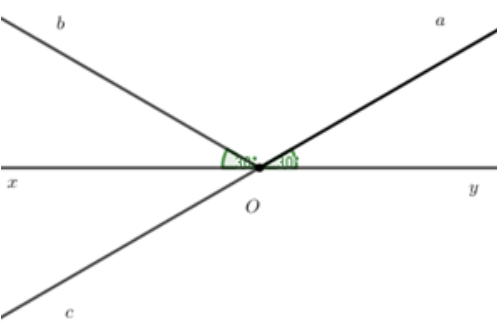
Đề bài

Bài 1. (2,0 điểm) Tính:

a) $A = \frac{{11}}{5} - \frac{7}{5}.\frac{3}{4};$

b) $B = 2022 - 40\%  + \frac{3}{5}.{( - 1)^{2021}}$

c) $C = \frac{{ - 8}}{{15}}.\frac{4}{{11}} + \frac{{ - 8}}{{15}}.\frac{7}{{11}} + 3\frac{8}{{15}};$

d) $D = \frac{3}{{2.6}} + \frac{3}{{6.10}} + \frac{3}{{10.14}} + ... + \frac{3}{{26.30}}$

Bài 2. (2,5 điểm) Tìm x, biết:

a) $\frac{3}{5} + \frac{2}{5}x = 1$;

b) $\frac{{2x - 6}}{3} = \frac{{x + 2}}{4}$;

c) $\left| {4x - 3} \right| = \frac{3}{2}:\frac{9}{8}$;

d) $\frac{{67}}{9} - {\left( {x - \frac{1}{6}} \right)^2} = \frac{1}{3}$.

Bài 3. (2,5 điểm) Một nhóm thiện nguyện tham gia chiến dịch “Giải cứu thanh long” trong vòng 3 tuần. Tuần đầu nhóm bán được $\frac{1}{3}$ tổng khối lượng thanh long, tuần thứ hai nhóm bán được $\frac{5}{8}$ khối lượng thanh long còn lại sau tuần đầu. Tuần thứ ba nhóm bán nốt 3 tấn thì vừa hết.

a) Hỏi tổng khối lượng thanh long nhóm thiện nguyện đã bán được?

b) Tính tỉ số phần trăm khối lượng thanh long bán được trong tuần thứ ba so với khối lượng thanh long bán được trong tuần thứ hai.

Bài 4. (2,5 điểm) Cho điểm O thuộc đường thẳng xy, vẽ tia Oa sao cho $\widehat {yOa}{\rm{ }} = {\rm{ }}{30^0}$.

a) Tính số đo $\widehat {xOa}$

b) Trên cùng một nửa mặt phẳng bờ là đường thẳng xy có chứa tia Oa, vẽ tia Ob sao cho $\widehat {xOb} = {30^0}$.  Tính số đo góc $\widehat {aOb}$

c) Vẽ tia Oc là tia đối của tia Oa. Chứng minh rằng Ox là tia phân giác của $\widehat {bOc}$

Bài 5. (0,5 điểm) Cho $S = \frac{1}{{{5^2}}} + \frac{1}{{{7^2}}} + \frac{1}{{{9^2}}} + ... + \frac{1}{{{{103}^2}}}$. Chứng minh rằng $S < \frac{5}{{32}}$.

LG bài 1

Phương pháp giải:

Thực hiện phép tính theo thứ tự:

Trong ngoặc => lũy thừa => Nhân, chia => Cộng, trừ

Lời giải chi tiết:

a)

$\begin{array}{l}A = \frac{{11}}{5} - \frac{7}{5}.\frac{3}{4}\\A = \frac{{11}}{5} - \frac{{21}}{{20}}\\A = \frac{{44}}{{20}} - \frac{{21}}{{20}}\\A = \frac{{23}}{{20}}\end{array}$

b)

$\begin{array}{l}B = 2022 - 40\%  + \frac{3}{5}.{( - 1)^{2021}}\\B = 2022 - \frac{{40}}{{100}} + \frac{3}{5}.( - 1)\\B = 2022 - \frac{2}{5} - \frac{3}{5}\\B = 2022 - \left( {\frac{2}{5} + \frac{3}{5}} \right)\\B = 2022 - 1\\B = 2021\end{array}$

c)

 $\begin{array}{l}C = \frac{{ - 8}}{{15}}.\frac{4}{{11}} + \frac{{ - 8}}{{15}}.\frac{7}{{11}} + 3\frac{8}{{15}}\\C = \frac{{ - 8}}{{15}}.\left( {\frac{4}{{11}} + \frac{7}{{11}}} \right) + 3\frac{8}{{15}}\\C = \frac{{ - 8}}{{15}}.1 + 3 + \frac{8}{{15}}\\C = \frac{{ - 8}}{{15}} + \frac{8}{{15}} + 3\\C = 3\end{array}$

d)

 $\begin{array}{l}D = \frac{3}{{2.6}} + \frac{3}{{6.10}} + \frac{3}{{10.14}} + ... + \frac{3}{{26.30}}\\D = 3.\left( {\frac{1}{{2.6}} + \frac{1}{{6.10}} + \frac{1}{{10.14}} + ... + \frac{1}{{26.30}}} \right)\\D = \frac{3}{4}.\left( {\frac{4}{{2.6}} + \frac{4}{{6.10}} + \frac{4}{{10.14}} + ... + \frac{4}{{26.30}}} \right)\\D = \frac{3}{4}.\left( {\frac{4}{2} - \frac{4}{6} + \frac{4}{6} - \frac{4}{{10}} + \frac{4}{{10}} - \frac{4}{{14}} + ... + \frac{4}{{26}} + \frac{4}{{30}}} \right)\\D = \frac{3}{4}.\left( {\frac{4}{2} - \frac{4}{{30}}} \right)\\D = \frac{3}{4}.\frac{{28}}{{15}}\\D = \frac{7}{5}\end{array}$

LG bài 2

Phương pháp giải:

a) Chuyển vế đổi dấu

b) $\frac{a}{b} = \frac{c}{d} \Rightarrow a.d = b.c$

c) |a|=m thì a=m hoặc a=-m

d) a²=m, m>0 thì a=m hoặc a=-m

Lời giải chi tiết:

a)

 $\begin{array}{l}\frac{3}{5} + \frac{2}{5}x = 1\\ \Rightarrow \frac{2}{5}x = 1 - \frac{3}{5}\\ \Rightarrow \frac{2}{5}x = \frac{2}{5}\\ \Rightarrow x = 1\end{array}$;

Vậy $x = 1$.

b)

$\begin{array}{l}\frac{{2x - 6}}{3} = \frac{{x + 2}}{4}\\ \Rightarrow 4.\left( {2x - 6} \right) = 3.\left( {x + 2} \right)\\ \Rightarrow 8x - 24 = 3x + 6\\ \Rightarrow 8x - 3x = 6 + 24\\ \Rightarrow 5x = 30\\ \Rightarrow x = 6\end{array}$

Vậy $x = 6$

c)

$\begin{array}{l}\left| {4x - 3} \right| = \frac{3}{2}:\frac{9}{8}\\ \Rightarrow \left| {4x - 3} \right| = \frac{3}{2}.\frac{8}{9}\\ \Rightarrow \left| {4x - 3} \right| = \frac{4}{3}\\ \Rightarrow \left[ {\begin{array}{*{20}{c}}{4x - 3 = \frac{4}{3}}\\{4x - 3 =  - \frac{4}{3}}\end{array}} \right.\\ \Rightarrow \left[ {\begin{array}{*{20}{c}}{4x = \frac{{13}}{3}}\\{4x = \frac{5}{3}}\end{array} \Rightarrow \left[ {\begin{array}{*{20}{c}}{x = \frac{{13}}{{12}}}\\{x = \frac{5}{{12}}}\end{array}} \right.} \right.\end{array}$

Vậy $x \in \left\{ {\frac{{13}}{{12}};\,\,\frac{5}{{12}}} \right\}$

d)

 $\begin{array}{l}\frac{{67}}{9} - {\left( {x - \frac{1}{6}} \right)^2} = \frac{1}{3}\\{\left( {x - \frac{1}{6}} \right)^2} = \frac{{67}}{9} - \frac{1}{3}\\{\left( {x - \frac{1}{6}} \right)^2} = \frac{{64}}{9}\\ \Rightarrow \left[ {\begin{array}{*{20}{c}}{x - \frac{1}{6} = \frac{8}{3}}\\{x - \frac{1}{6} = \frac{{ - 8}}{3}}\end{array}} \right.\\ \Rightarrow \left[ {\begin{array}{*{20}{c}}{x = \frac{8}{3} + \frac{1}{6}}\\{x = \frac{1}{6} - \frac{8}{3}}\end{array}} \right.\\ \Rightarrow \left[ {\begin{array}{*{20}{c}}{x = \frac{{17}}{6}}\\{x = \frac{{ - 5}}{2}}\end{array}} \right.\end{array}$

Vậy $x \in \left\{ {\frac{{17}}{6};\,\frac{{ - 5}}{2}} \right\}$

LG bài 3

Phương pháp giải:

a) Tính số phần thanh long bán được trong ngày thứ ba

=> Tổng khối lượng thanh long bán được cả ba ngày

b) Tính khối lượng thanh long bán được trong tuần 2.

=> Tỉ số phần trăm khối lượng thanh long bán được trong tuần thứ ba so với khối lượng thanh long bán được trong tuần thứ hai

Lời giải chi tiết:

a) Số phần thanh long bán được trong ngày thứ ba là:

$1 - \frac{1}{3} - \frac{5}{8} = \frac{1}{{24}}$

Tổng khối lượng thanh long bán được là:

$3:\frac{1}{{24}} = 72$(tấn)

b)

Khối lượng thanh long bán được trong tuần 2 là:

$72.\frac{5}{8} = 45$ (tấn)

Tỉ số phần trăm khối lượng thanh long bán được trong tuần thứ ba so với khối lượng thanh long bán được trong tuần thứ hai là: $\frac{3}{{45}} = \frac{1}{{15}}$

LG bài 4

Phương pháp giải:

- Tổng hai góc kề bù bằng 180 độ

- Trên cùng một nửa mặt phẳng có bờ chứa tia Ox có:

$\widehat {xOy} < \widehat {xOz}$

=> Tia Oy nằm giữa hai tia Ox và Oz.

- Nếu tia Oy nằm giữa hai tia Ox và Oz và $\widehat {yOx} = \widehat {yOx}$ thì Oy là tia phân giác của góc xOz.

Lời giải chi tiết:

a) Do $\widehat {yOa}$ và $\widehat {xOa}$ là hai góc kề bù nên:

$\widehat {yOa}$ + $\widehat {xOa}$ = ${180^0}$

${30^0}$ + $\widehat {xOa}$ = ${180^0}$

$\widehat {xOa}$ = ${150^0}$

b)

Trên cùng một nửa mặt phẳng có bờ chứa tia Ox có:

$\widehat {xOb} < \widehat {xOa}\,\,({30^0} < {150^0})$

Nên tia Ob nằm giữa hai tia Ox và Oa

$\begin{array}{l} \Rightarrow \widehat {xOb} + \widehat {aOb} = \widehat {xOa}\\ \Rightarrow {30^0} + \widehat {aOb} = {150^0}\\ \Rightarrow \widehat {aOb} = {120^0}\end{array}$

c)

Ta có: $\widehat {aOb} + \widehat {bOc} = {180^0}$(Kề bù)

$\begin{array}{l} \Rightarrow {120^0} + \widehat {bOc} = {180^0}\\ \Rightarrow \widehat {bOc} = {60^0}\end{array}$

Trên cùng một nửa mặt phẳng có bờ chứa tia Ob có:

$\widehat {bOx} < \widehat {bOc}({30^0} < {60^0})$

=> Tia Ox nằm giữa hai tia Ob và Oc (1)

 $\begin{array}{l}\widehat {bOx} + \widehat {xOc} = \widehat {bOc}\\ \Rightarrow {30^0} + \widehat {xOc} = {60^0}\\ \Rightarrow \widehat {xOc} = {30^0}\\ \Rightarrow \widehat {xOc} = \widehat {xOb} = {30^0}\,\,(2)\end{array}$

Từ (1) và (2) suy ra Ox là phân giác của $\widehat {bOc}$.

LG bài 5

Phương pháp giải:

Áp dụng:

$\frac{1}{{{n^2}}} < \frac{1}{{(n - 1).(n + 1)}}$

Lời giải chi tiết:

Ta có:

$\begin{array}{l}\frac{1}{{{5^2}}} < \frac{1}{{4.6}}\\\frac{1}{{{7^2}}} < \frac{1}{{6.8}}\\\frac{1}{{{9^2}}} < \frac{1}{{8.10}}\\..........\\\frac{1}{{{{103}^2}}} < \frac{1}{{102.104}}\\\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\\ \Rightarrow S < \frac{1}{{4.6}} + \frac{1}{{6.8}} + \frac{1}{{8.10}} + .... + \frac{1}{{102.104}}\\ \Rightarrow S < \frac{1}{2}.\left( {\frac{1}{4} - \frac{1}{6} + \frac{1}{6} - \frac{1}{8} + \frac{1}{8} - \frac{1}{{10}} + ... + \frac{1}{{102}} - \frac{1}{{104}}} \right)\\ \Rightarrow S < \frac{1}{2}.\left( {\frac{1}{4} - \frac{1}{{104}}} \right)\\ \Rightarrow S < \frac{{25}}{{208}} < \frac{{25}}{{160}}\\ \Rightarrow S < \frac{5}{{32}}\end{array}$

HocTot.Nam.Name.Vn