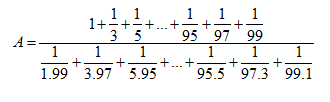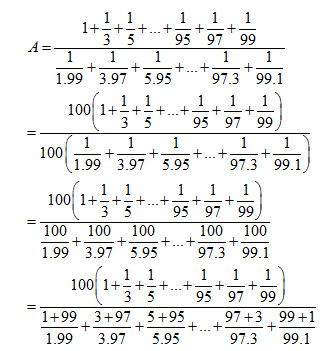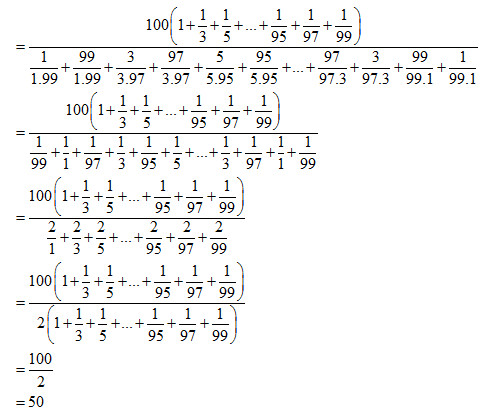Đề thi học kì 2 môn toán lớp 6 năm 2019 - 2020 trường THCS Giảng Võ

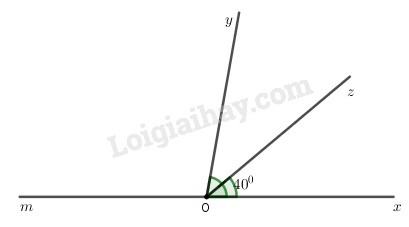
Đề bài

Bài 1  (3,0 điểm):

Thực hiện phép tính (Tính hợp lý nếu có thể)

a) $\dfrac{4}{5} - \dfrac{7}{6} + \dfrac{{ - 6}}{{15}}$

b) $\dfrac{{ - 5}}{9}.\dfrac{7}{{13}} + \dfrac{6}{{13}}.\dfrac{{ - 5}}{9} + 3\dfrac{7}{9}$

c) $6\dfrac{3}{8} - \left( {4\dfrac{3}{8} - \dfrac{1}{2}} \right)$

d) $2\dfrac{1}{3}.1,5 - \left( {\dfrac{{11}}{{10}} + 50\% } \right):\dfrac{4}{{15}}$

Bài 2 (2,5 điểm):

Tìm $x$ biết:

a) $\dfrac{3}{2} + x =  - \dfrac{5}{3}$

b) $5\dfrac{2}{3} - \left( {\dfrac{3}{2} + x} \right) = 4\dfrac{1}{3}$

c) $\left| {x - \dfrac{1}{2}} \right| + 75\%  = \dfrac{9}{{10}}$

Bài 3 (2,0 điểm):

Trong đợt phát động phong trào thu gom giấy vụn làm kế hoạch nhỏ của các bạn học sinh một trường THCS, ban tổ chức tổng kết như sau:

Tổng số giấy vụn thu được là 870kg, trong đó số kg giấy vụn khối 6 thu được bằng $\dfrac{2}{5}$ tổng số, số kg giấy vụn khối 7 thu được bằng $50\%$ số kg giấy vụn khối 6 thu được, còn lại là của khối 8 và khối 9 thu được.

a) Tính số kg giấy vụn của cả khối 8 và khối 9 thu được

b) Số kg giấy vụn khối 6 thu được chiếm bao nhiêu phần trăm so với tổng số kg giấy vụn cả trường thu được.

Bài 4 (2 điểm): Cho $\widehat {xOy} = {80^0}$ và tia $Oz$ nằm giữa hai tia $Ox,Oy$ sao cho $\widehat {xOz} = {40^0}.$

a) Tính số đo $\widehat {zOy}?$

b) Chứng tỏ rằng: Tia $Oz$ là tia phân giác của $\widehat {xOy}.$

c) Vẽ tia $Om$ là tia đối của tia $Ox.$ Tính số đo $\widehat {mOz}?$

Bài 5 (0,5 điểm):

Tính giá trị biểu thức:  

HẾT

LG bài 1

Phương pháp giải:

a) Quy đồng mẫu rồi thực hiện cộng, trừ các phân số cùng mẫu

b) Sử dụng tính chất $ab + ac = a.\left( {b + c} \right)$ 

c) Sử dụng quy tắc phá ngoặc rồi thực hiện phép tính từ trái qua phải

d) Đổi các số về phân số, rồi thực hiện theo thứ tự trong ngoặc rồi đến nhân chia trước, cộng trừ sau.

Lời giải chi tiết:

a) $\dfrac{4}{5} - \dfrac{7}{6} + \dfrac{{ - 6}}{{15}}$

$\begin{array}{l} = \dfrac{{4.6}}{{5.6}} - \dfrac{{7.5}}{{6.5}} + \dfrac{{ - 6.2}}{{15.2}}\\ = \dfrac{{24}}{{30}} - \dfrac{{35}}{{30}} + \dfrac{{ - 12}}{{30}}\\ = \dfrac{{24 - 35 + \left( { - 12} \right)}}{{30}}\\ = \dfrac{{ - 23}}{{30}}\end{array}$

b) $\dfrac{{ - 5}}{9}.\dfrac{7}{{13}} + \dfrac{6}{{13}}.\dfrac{{ - 5}}{9} + 3\dfrac{7}{9}$

$\begin{array}{l} = \dfrac{{ - 5}}{9}\left( {\dfrac{7}{{13}} + \dfrac{6}{{13}}} \right) + 3\dfrac{7}{9}\\ = \dfrac{{ - 5}}{9}.\dfrac{{13}}{{13}} + \dfrac{{34}}{9}\\ = \dfrac{{ - 5}}{9}.1 + \dfrac{{34}}{9}\\ = \dfrac{{ - 5}}{9} + \dfrac{{34}}{9}\\ = \dfrac{{ - 5 + 34}}{9}\\ = \dfrac{{29}}{9}\end{array}$

c) $6\dfrac{3}{8} - \left( {4\dfrac{3}{8} - \dfrac{1}{2}} \right)$

$\begin{array}{l} = 6\dfrac{3}{8} - 4\dfrac{3}{8} + \dfrac{1}{2}\\ = \left( {6 - 4} \right) + \left( {\dfrac{3}{8} - \dfrac{3}{8}} \right) + \dfrac{1}{2}\\ = 2 + \dfrac{1}{2}\\ = \dfrac{4}{2} + \dfrac{1}{2} = \dfrac{5}{2}\end{array}$ 

d) $2\dfrac{1}{3}.1,5 - \left( {\dfrac{{11}}{{10}} + 50\% } \right):\dfrac{4}{{15}}$

$\begin{array}{l} = \dfrac{7}{3}.\dfrac{{15}}{{10}} - \left( {\dfrac{{11}}{{10}} + \dfrac{1}{2}} \right):\dfrac{4}{{15}}\\ = \dfrac{7}{2} - \left( {\dfrac{{11}}{{10}} + \dfrac{5}{{10}}} \right).\dfrac{{15}}{4}\\ = \dfrac{7}{2} - \dfrac{{16}}{{10}}.\dfrac{{15}}{4}\\ = \dfrac{7}{2} - \dfrac{8}{5}.\dfrac{{15}}{4}\\ = \dfrac{7}{2} - 6\\ = \dfrac{7}{2} - \dfrac{{12}}{2}\\ = \dfrac{{ - 5}}{2}\end{array}$

LG bài 2

Phương pháp giải:

a) Muốn tìm số hạng chưa biết ta lấy tổng trừ số hạng đã biết

b) Muốn tìm số trừ ta lấy số bị trừ trừ đi hiệu

Muốn tìm số hạng chưa biết ta lấy tổng trừ số hạng đã biết

c) Sử dụng $\left| A \right| = m\left( {m \ge 0} \right)$ thì $A = m$ hoặc $A =  - m$

Lời giải chi tiết:

a) $\dfrac{3}{2} + x =  - \dfrac{5}{3}$

$\begin{array}{l}x =  - \dfrac{5}{3} - \dfrac{3}{2}\\x = \dfrac{{ - 10}}{6} - \dfrac{9}{6}\\x = \dfrac{{ - 10 - 9}}{6}\\x = \dfrac{{ - 19}}{6}\end{array}$

Vậy $x =  - \dfrac{{19}}{6}.$

b) $5\dfrac{2}{3} - \left( {\dfrac{3}{2} + x} \right) = 4\dfrac{1}{3}$

$\begin{array}{l}\dfrac{3}{2} + x = 4\dfrac{1}{3} - 5\dfrac{2}{3}\\\dfrac{3}{2} + x = \dfrac{{13}}{3} - \dfrac{{17}}{3}\\\dfrac{3}{2} + x = \dfrac{{ - 4}}{3}\\x = \dfrac{{ - 4}}{3} - \dfrac{3}{2}\\x = \dfrac{{ - 8}}{6} - \dfrac{9}{6}\\x = \dfrac{{ - 8 - 9}}{6}\\x = \dfrac{{ - 17}}{6}\end{array}$

Vậy $x =  - \dfrac{{17}}{6}.$

c) $\left| {x - \dfrac{1}{2}} \right| + 75\%  = \dfrac{9}{{10}}$

$\begin{array}{l}\left| {x - \dfrac{1}{2}} \right| + \dfrac{{75}}{{100}} = \dfrac{9}{{10}}\\\left| {x - \dfrac{1}{2}} \right| = \dfrac{9}{{10}} - \dfrac{{75}}{{100}}\\\left| {x - \dfrac{1}{2}} \right| = \dfrac{9}{{10}} - \dfrac{3}{4}\\\left| {x - \dfrac{1}{2}} \right| = \dfrac{{18}}{{20}} - \dfrac{{15}}{{20}}\\\left| {x - \dfrac{1}{2}} \right| = \dfrac{3}{{20}}\end{array}$

TH1:

 $\begin{array}{l}x - \dfrac{1}{2} = \dfrac{3}{{20}}\\x = \dfrac{3}{{20}} + \dfrac{1}{2}\\x = \dfrac{3}{{20}} + \dfrac{{10}}{{20}}\\x = \dfrac{{13}}{{20}}\end{array}$

TH2: 

 $\begin{array}{l}x - \dfrac{1}{2} =  - \dfrac{3}{{20}}\\x =  - \dfrac{3}{{20}} + \dfrac{1}{2}\\x =  - \dfrac{3}{{20}} + \dfrac{{10}}{{20}}\\x = \dfrac{7}{{20}}\end{array}$

Vậy $x = \dfrac{{13}}{{30}};x = \dfrac{7}{{20}}$

LG bài 3

Phương pháp giải:

Giá trị phân số $\dfrac{m}{n}$ của 1 số $a$ cho trước là $a.\dfrac{m}{n}$

Tỉ số phần trăm của hai số $a$ và $b$ là $\dfrac{{a.100}}{b}\%$

Lời giải chi tiết:

a) Tính số kg giấy vụn của cả khối 8 và khối 9 thu được

Số kg giấy vụn của khối 6 thu được là: $\dfrac{2}{5}.870 = 348$ kg

Số kg giấy vụn của khối 7 thu được là: $50\% .348 = \dfrac{1}{2}.348$ $= 174$ kg

Số kg giấy vụn của cả khối 8 và khối 9 thu được là: $870 - \left( {348 + 174} \right) = 318$ kg

b) Số kg giấy vụn khối 6 thu được chiếm bao nhiêu phần trăm so với tổng số kg giấy vụn cả trường thu được.

Số kg giấy vụn khối 6 thu được chiếm số phần trăm so với tổng số kg giấy vụn cả trường thu được là:

$\dfrac{{348.100}}{{870}}\%  = 40\%$

LG bài 4

Phương pháp giải:

a) Chứng minh tia On nằm giữa hai tia Ox và Om.

Sử dụng đẳng thức cộng góc $\widehat {xOn} + \widehat {nOm} = \widehat {xOm}$.

b) Chứng minh tia On nằm giữa hai tia Ox và Om và góc $\widehat {xOn} = \widehat {nOm}$.

c) Nhận xét hai góc $\widehat {xOn}$ và $\widehat {nOy}$ là hai góc kề bù.

Sử dụng tính chất hai góc kề bù có tổng số đo bằng ${180^0}$.

d) Chứng minh tia Ox nằm giữa hai tia On và Oz.

Sử dụng đẳng thức cộng góc: $\widehat {xOn} + \widehat {xOz} = \widehat {nOz}$.

Lời giải chi tiết:

Cho $\widehat {xOy} = {80^0}$ và tia $Oz$ nằm giữa hai tia $Ox,Oy$ sao cho $\widehat {xOz} = {40^0}.$

a) Tính số đo $\widehat {zOy}?$

Trên cùng một nửa mặt phẳng bờ là đường thẳng chưa tia Ox, tia Oz nằm giữa hai tia Ox và Oy nên ta có:

$\begin{array}{l}\widehat {xOz} + \widehat {zOy} = \widehat {xOy}\\ \Rightarrow {40^0} + \widehat {zOy} = {80^0}\\ \Rightarrow \widehat {zOy} = {80^0} - {40^0}\\ \Rightarrow \widehat {zOy} = {40^0}\end{array}$

Vậy $\widehat {zOy} = {40^0}$.

b) Chứng tỏ rằng: Tia $Oz$ là tia phân giác của $\widehat {xOy}.$

Ta có: tia $Oz$ nằm giữa hai tia $Ox$ và $Oy$

$\widehat {xOz} = \widehat {zOy} = {40^0}^0$

Vậy tia $Oz$ là tia phân giác của $\widehat {xOy}$.

c) Vẽ tia $Om$ là tia đối của tia $Ox.$ Tính số đo $\widehat {mOz}?$

Tia $Om$ là tia đối của tia $Ox$ nên $\widehat {xOm} = {180^0}$.

Hai góc $\widehat {xOz}$ và $\widehat {zOm}$ là hai góc kề bù nên

$\widehat {xOz} + \widehat {zOm} = {180^0}$ (tính chất hai góc kề bù)

$\begin{array}{l} \Rightarrow {40^0} + \widehat {zOm} = {180^0}\\ \Rightarrow \widehat {zOm} = {180^0} - {40^0}\\ \Rightarrow \widehat {zOm} = {140^0}\end{array}$

Vậy $\widehat {zOm} = {140^0}$.

LG bài 5

Phương pháp giải:

Nhân của tử và mẫu của biểu thức với $100$ và biến đổi mẫu số.

Lời giải chi tiết:

Ta có

HẾT

HocTot.Nam.Name.Vn