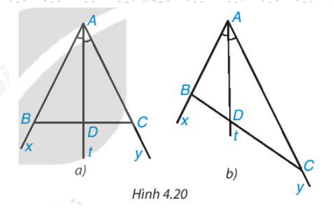
Giải câu hỏi trang 84, 85 SGK Toán 8 tập 1 - Kết nối tri thứcCho tia phân giác At của góc xAy (H.4.20). Nếu lấy điểm B trên tia Ax, điểm C trên tia Ay, ta được tam giác ABC. Giả sử tia phân giác At cắt BC tại điểm D. Khi lấy B và C sao cho AB = AC (H.4.20a), hãy so sánh tỉ số (dfrac{{DB}}{{DC}}) và (dfrac{{AB}}{{AC}}) Tổng hợp đề thi học kì 1 lớp 8 tất cả các môn - Kết nối tri thức Toán - Văn - Anh - Khoa học tự nhiên
Lựa chọn câu để xem lời giải nhanh hơn
HĐ1 Video hướng dẫn giải Cho tia phân giác At của góc xAy (H.4.20). Nếu lấy điểm B trên tia Ax, điểm C trên tia Ay, ta được tam giác ABC. Giả sử tia phân giác At cắt BC tại điểm D. Khi lấy B và C sao cho AB = AC (H.4.20a), hãy so sánh tỉ số \(\dfrac{{DB}}{{DC}}\) và \(\dfrac{{AB}}{{AC}}\) Phương pháp giải: Vận dụng tính chất đường phân giác của tam giác. Lời giải chi tiết: Theo đề bài, At là tia phân giác của góc xAy hay AD là tia phân giác của góc BAC. Tam giác ABC cân tại A (vì AB = AC) có AD là tia phân giác của góc BAC nên AD cũng là đường trung tuyến của tam giác ABC. Suy ra D là trung điểm của cạnh BC hay DB = DC nên \(\dfrac{{DB}}{{DC}} = 1\). Vì AB = AC nên \(\dfrac{{AB}}{{AC}} = 1\) Vậy khi lấy B và C sao cho AB = AC thì \(\dfrac{{DB}}{{DC}} = \dfrac{{AB}}{{AC}}\) HĐ2 Video hướng dẫn giải Cho tia phân giác At của góc xAy (H.4.20). Nếu lấy điểm B trên tia Ax, điểm C trên tia Ay, ta được tam giác ABC. Giả sử tia phân giác At cắt BC tại điểm D Khi lấy B và C sao cho AB = 2 cm và AC = 4 cm (H.4.20b), hãy dùng thước có vạch chia đến milimét để đo độ dài các đoạn thẳng DB, DC rồi so sánh hai tỉ số \(\dfrac{{DB}}{{DC}}\) và \(\dfrac{{AB}}{{AC}}\) Phương pháp giải: Dùng thước đo các khoảng cách và tính tỉ số Lời giải chi tiết: Dùng thước có vạch chia đến milimét để đo độ dài các đoạn thẳng DB, DC, ta được: DB = 12 mm = 1,2 cm và DC = 24 mm = 2,4 cm. Khi đó, \(\dfrac{{DB}}{{DC}} = \dfrac{{1,2}}{{2,4}} = \dfrac{1}{2};\dfrac{{AB}}{{AC}} = \dfrac{2}{4} = \dfrac{1}{2}\) Vậy khi lấy B và C sao cho AB = 2 cm và AC = 4 cm thì \(\dfrac{{DB}}{{DC}} = \dfrac{{AB}}{{AC}}\) Luyện tập Video hướng dẫn giải Tính độ dài x trên Hình 4.23 Phương pháp giải: Vận dụng tính chất đường phân giác trong tam giác Lời giải chi tiết: Trong Hình 4.23 có \(\widehat {DME} = \widehat {MEF}\) nên EM là tia phân giác của \(\widehat {{\rm{DEF}}}\). Áp dụng tính chất đường phân giác của tam giác, ta có: \(\dfrac{{E{\rm{D}}}}{{EF}} = \dfrac{{M{\rm{D}}}}{{MF}}\) hay \(\dfrac{{4,5}}{x} = \dfrac{{3,5}}{{5,6}}\) Suy ra: \(x = \dfrac{{5,6.4,5}}{{3,5}} = 7,2\)(đvđd) Vậy x = 7,2 (đvđd).
|