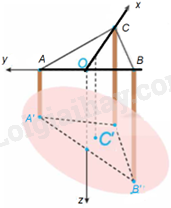
Giải bài tập 5.50 trang 63 SGK Toán 12 tập 2 - Kết nối tri thứcTừ mặt nước trong một bể nước, tại ba vị trí đôi một cách nhau 2m, người ta lần lượt thả dây dọi để quả dọi chạm đáy bể. Phần dây dọi (thẳng) nằm trong nước tại ba vị trí đó lần lượt có độ dài 4m; 4,4m; 4,8m. Biết đáy bể là phẳng. Hỏi đáy bể nghiêng so với mặt phẳng nằm ngang một góc bao nhiêu độ? Tổng hợp đề thi học kì 2 lớp 12 tất cả các môn - Kết nối tri thức Toán - Văn - Anh - Hoá - Sinh - Sử - Địa Đề bài Từ mặt nước trong một bể nước, tại ba vị trí đôi một cách nhau 2 m, người ta lần lượt thả dây dọi để quả dọi chạm đáy bể. Phần dây dọi (thẳng) nằm trong nước tại ba vị trí đó lần lượt có độ dài 4 m; 4,4 m; 4,8 m. Biết đáy bể là phẳng. Hỏi đáy bể nghiêng so với mặt phẳng nằm ngang một góc bao nhiêu độ? Phương pháp giải - Xem chi tiết Sử dụng kiến thức về góc giữa hai mặt phẳng để tính: Trong không gian Oxyz, cho hai mặt phẳng (P), (Q) tương ứng có các vectơ pháp tuyến là →n=(A;B;C),→n′=(A′;B′;C′). Khi đó, góc giữa (P) và (Q), kí hiệu là ((P), (Q)) được tính theo công thức: cos((P),(Q))=|cos(→n,→n′)|=|AA′+BB′+CC′|√A2+B2+C2.√A′2+B′2+C′2. Lời giải chi tiết Gọi 3 điểm cách nhau 2m trên mặt nước là A, B, C. Vị trí thả quả rọi xuống đáy bể lần lượt là A’, B’, C’ sao cho AA' = 4 m, BB' = 4,4 m, CC' = 4,8 m. Chọn gốc tọa độ O tại trung điểm AB.
Khi đó, A(0;1;0) B(0;-1;0) C(√3;0;0); A’(0;1;4); B’(0;-1;4,4); C’ (√3;0; 4,8). Ta có: →A′B′=(0;−2;0,4);→B′C′=(√3;1;0,4). Mặt phẳng (A’B’C’) nhận [→A′B′;→B′C′] làm một vectơ pháp tuyến. Ta có: [→A′B′;→B′C′]=(|−20,410,4|;|0,400,4√3|;|0−2√31|)=(−65;2√35;2√3). Mặt phẳng đáy bể là mặt phẳng (A’ B’ C’) nên có vectơ pháp tuyến là →n=(−65;2√35;2√3). Mặt phẳng ngang (mặt nước) là mặt phẳng (Oxy) có vectơ pháp tuyến là →k=(0;0;1). Nên góc giữa mặt phẳng đáy bể và mặt phẳng ngang là: cos((A′B′C′),(Oxy))=|−65.0+2√35.0+2√3.1|√(−65)2+(2√35)2+(2√3)2.√02+02+12=5√2929. ⇒((A′B′C′),(Oxy))≈21,80. Vậy đáy bể nghiêng so với mặt phẳng nằm ngang một góc khoảng 21,8 độ.
|