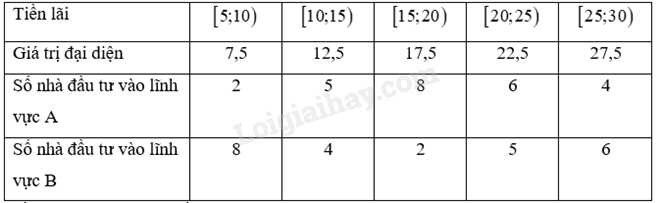
Giải bài tập 3.15 trang 86 SGK Toán 12 tập 1 - Kết nối tri thứcNgười ta ghi lại tiền lãi (đơn vị: triệu đồng) của một số nhà đầu tư (với số tiền đầu tư như nhau), khi đầu tư vào hai lĩnh vực A, B cho kết quả như sau: a) Về trung bình, đầu tư vào lĩnh vực nào đem lại tiền lãi cao hơn? b) Tính độ lệch chuẩn cho các mẫu số liệu về tiền lãi của các nhà đầu tư ở hai lĩnh vực này và giải thích ý nghĩa của các số thu được. Tổng hợp đề thi học kì 1 lớp 12 tất cả các môn - Kết nối tri thức Toán - Văn - Anh - Lí - Hóa - Sinh - Sử - Địa Đề bài
Người ta ghi lại tiền lãi (đơn vị: triệu đồng) của một số nhà đầu tư (với số tiền đầu tư như nhau), khi đầu tư vào hai lĩnh vực A, B cho kết quả như sau: a) Về trung bình, đầu tư vào lĩnh vực nào đem lại tiền lãi cao hơn? b) Tính độ lệch chuẩn cho các mẫu số liệu về tiền lãi của các nhà đầu tư ở hai lĩnh vực này và giải thích ý nghĩa của các số thu được. Phương pháp giải - Xem chi tiết + Sử dụng kiến thức về phương sai của mẫu số liệu ghép nhóm để tính: Phương sai của mẫu số liệu ghép nhóm, kí hiệu là \({s^2}\), là một số được tính theo công thức sau: \({s^2} = \frac{1}{n}\left( {{m_1}x_1^2 + ... + {m_k}x_k^2} \right) - {\left( {\overline x } \right)^2}\), trong đó \(n = {m_1} + ... + {m_k}\) với \(\overline x = \frac{{{m_1}{x_1} + ... + {m_k}{x_k}}}{n}\) là số trung bình của mẫu số liệu ghép nhóm. + Sử dụng kiến thức độ lệch chuẩn của mẫu số liệu ghép nhóm để tính: Độ lệch chuẩn của mẫu số liệu ghép nhóm, kí hiệu là s, là căn bậc hai số học của phương sai của mẫu số liệu ghép nhóm, tức là \(s = \sqrt {{s^2}} \). + Sử dụng kiến thức về ý nghĩa của độ lệch chuẩn để giải thích: Độ lệch chuẩn của mẫu số liệu ghép nhóm càng lớn thì độ rủi ro càng lớn. Lời giải chi tiết a) Ta có mẫu số liệu ghép nhóm với giá trị đại diện là: Tiền lãi trung bình khi đầu tư vào lĩnh vực A là: \(\overline {{x_A}} = \frac{{7,5.2 + 12,5.5 + 17,5.8 + 22,5.6 + 27,5.4}}{{2 + 5 + 8 + 6 + 4}} = 18,5\) (triệu đồng) Tiền lãi trung bình khi đầu tư vào lĩnh vực B là: \(\overline {{x_B}} = \frac{{7,5.8 + 12,5.4 + 17,5.2 + 22,5.5 + 27,5.6}}{{8 + 4 + 2 + 5 + 6}} = 16,9\) (triệu đồng) Do đó, về trung bình, đầu tư vào lĩnh vực A đem lại tiền lãi cao hơn. b) Phương sai của mẫu số liệu về tiền lãi khi đầu tư vào lĩnh vực A: \(s_A^2 = \frac{1}{{25}}\left( {7,{5^2}.2 + 12,{5^2}.5 + 17,{5^2}.8 + 22,{5^2}.6 + 27,{5^2}.4} \right) - 18,{5^2} = 34\) Độ lệch chuẩn của mẫu số liệu về tiền lãi khi đầu tư vào lĩnh vực A: \({s_A} = \sqrt {34} \) (triệu đồng) Phương sai của mẫu số liệu về tiền lãi khi đầu tư vào lĩnh vực B: \(s_B^2 = \frac{1}{{25}}\left( {7,{5^2}.8 + 12,{5^2}.4 + 17,{5^2}.2 + 22,{5^2}.5 + 27,{5^2}.6} \right) - 16,{9^2} = 64,64\) Độ lệch chuẩn của mẫu số liệu về tiền lãi khi đầu tư vào lĩnh vực B: \({s_B} = \sqrt {64,64} \) (triệu đồng) Như vậy, độ lệch chuẩn của mẫu số liệu về tiền lãi đầu tư vào lĩnh vực B lớn hơn độ lệch chuẩn của mẫu số liệu về tiền lãi đầu tư vào lĩnh vực A nên đầu tư vào lĩnh vực B là rủi ro hơn.
|