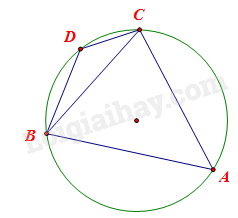
Giải bài tập 3 trang 78 SGK Toán 9 tập 2 - Cánh diềuCho tam giác ABC nội tiếp đường tròn (O) thỏa mãn (widehat {ABC} = 60^circ ,widehat {ACB} = 70^circ .) Giả sử D là điểm thuộc cung BC không chứa A (D khác B và C). Tính số đo góc BDC. Tổng hợp Đề thi vào 10 có đáp án và lời giải Toán - Văn - Anh Đề bài Cho tam giác ABC nội tiếp đường tròn (O) thỏa mãn ^ABC=60∘,^ACB=70∘.ˆABC=60∘,ˆACB=70∘. Giả sử D là điểm thuộc cung BC không chứa A (D khác B và C). Tính số đo góc BDC. Video hướng dẫn giải Phương pháp giải - Xem chi tiết Bước 1: Áp dụng Định lý tổng 3 góc trong tam giác ABC để tính góc A. Bước 2: Áp dụng tổng 2 góc đối trong tứ giác nội tiếp đường tròn bằng 180∘180∘ để tính góc BDC. Lời giải chi tiết
Áp dụng Định lý tổng 3 góc trong tam giác ABC có: ^ABC+^BCA+^CAB=180∘^CAB=180∘−^ABC−^BCA^CAB=180∘−60∘−70∘^CAB=50∘. Vì tứ giác ABDC nội tiếp đường tròn nên tổng 2 góc đối bằng 180∘, do đó ta có: ˆA+ˆD=180∘ˆD=180∘−ˆAˆD=180∘−50∘ˆD=130∘. Vậy ^BDC=130∘.  Chia sẻ Bình luận
Tham Gia Group 2K10 Ôn Thi Vào Lớp 10 Miễn Phí
>> Học trực tuyến Lớp 10 cùng thầy cô giáo giỏi tại Tuyensinh247.com, (Xem ngay) Cam kết giúp học sinh học tốt, bứt phá điểm 9,10 chỉ sau 3 tháng, làm quen kiến thức, định hướng luyện thi TN THPT, ĐGNL, ĐGTD ngay từ lớp 10
|
