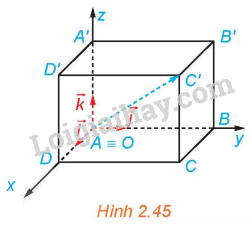
Giải bài tập 2.17 trang 65 SGK Toán 12 tập 1 - Kết nối tri thứcTrong không gian Oxyz, cho hình hộp chữ nhật ABCD.A’B’C’D’ có đỉnh A trùng với gốc O và các đỉnh D, B, A’ có tọa độ lần lượt là (2; 0; 0), (0; 4; 0), (0; 0; 3) (H.2.45). Xác định tọa độ của các đỉnh còn lại của hình hộp chữ nhật. Đề bài Trong không gian Oxyz, cho hình hộp chữ nhật ABCD.A’B’C’D’ có đỉnh A trùng với gốc O và các đỉnh D, B, A’ có tọa độ lần lượt là (2; 0; 0), (0; 4; 0), (0; 0; 3) (H.2.45). Xác định tọa độ của các đỉnh còn lại của hình hộp chữ nhật.
Phương pháp giải - Xem chi tiết Sử dụng kiến thức về tọa độ của điểm trong không gian để xác định tọa độ các điểm: Trong không gian Oxyz, cho một điểm M tùy ý. Bộ ba số (x; y; z) duy nhất sao cho \(\overrightarrow {OM} = x\overrightarrow i + y\overrightarrow j + z\overrightarrow k \) được gọi là tọa độ của điểm M đối với hệ tọa độ Oxyz. Khi đó, ta viết \(M = \left( {x;y;z} \right)\) hoặc \(M\left( {x;y;z} \right)\), trong đó x là hoành độ, y là tung độ, z là cao độ của M. Lời giải chi tiết Vì A trùng gốc O nên A(0; 0; 0). Vì D thuộc tia Ox nên hai vectơ \(\overrightarrow {OD} \) và \(\overrightarrow i \) cùng hướng. Do đó, tồn tại số thực m sao cho \(\overrightarrow {OD} = m\overrightarrow i \). Mà D(2; 0; 0) nên \(m = 2\). Vì B thuộc tia Oy nên hai vectơ \(\overrightarrow {OB} \) và \(\overrightarrow j \) cùng hướng. Do đó, tồn tại số thực n sao cho \(\overrightarrow {OB} = n\overrightarrow j \). Mà B(0; 4; 0) nên \(n = 4\) Vì A’ thuộc tia Oz nên hai vectơ \(\overrightarrow {OA'} \) và \(\overrightarrow k \) cùng hướng. Do đó, tồn tại số thực p sao cho \(\overrightarrow {OA'} = p\overrightarrow k \). Mà A’(0; 0; 3) nên \(p = 3\). Vì ODCB là hình bình hành nên \(\overrightarrow {OC} = \overrightarrow {OD} + \overrightarrow {OB} = m\overrightarrow i + n\overrightarrow j = 2\overrightarrow i + 4\overrightarrow j \). Do đó, C(2; 4; 0). Vì OA’B’B là hình bình hành nên \(\overrightarrow {OB'} = \overrightarrow {OA'} + \overrightarrow {OB} = p\overrightarrow k + n\overrightarrow j = 3\overrightarrow k + 4\overrightarrow j \). Do đó, B’(0; 4; 3). Vì OA’D’D là hình bình hành nên \(\overrightarrow {OD'} = \overrightarrow {OA'} + \overrightarrow {OD} = m\overrightarrow i + p\overrightarrow k = 2\overrightarrow i + 3\overrightarrow k \). Do đó, D’(2; 0; 3). Vì ABCD. A’B’C’D’ là hình hộp chữ nhật nên theo quy tắc hình hộp ta có: \(\overrightarrow {OC'} = \overrightarrow {OD} + \overrightarrow {OB} + \overrightarrow {OA'} = m\overrightarrow i + n\overrightarrow j + p\overrightarrow k = 2\overrightarrow i + 4\overrightarrow j + 3\overrightarrow k \). Do đó, C’(2; 4; 3).  Chia sẻ Bình luận
Group Ôn Thi ĐGNL & ĐGTD Miễn Phí
|
