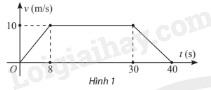
Giải bài tập 10 trang 29 SGK Toán 12 tập 2 - Chân trời sáng tạoTốc độ chuyển động (v{rm{ }}left( {{rm{m/s}}} right)) của một ca nô trong khoảng thời gian 40 giây được thể hiện như hình dưới đây. Quãng đường đi được của ca nô trong khoảng thời gian này là: A. 400 m B. 350 m C. 310 m D. 200 m Tổng hợp đề thi học kì 1 lớp 12 tất cả các môn - Chân trời sáng tạo Toán - Văn - Anh - Lí - Hóa - Sinh - Sử - Địa Đề bài Tốc độ chuyển động \(v{\rm{ }}\left( {{\rm{m/s}}} \right)\) của một ca nô trong khoảng thời gian 40 giây được thể hiện như hình 1. Quãng đường đi được của ca nô trong khoảng thời gian này là:
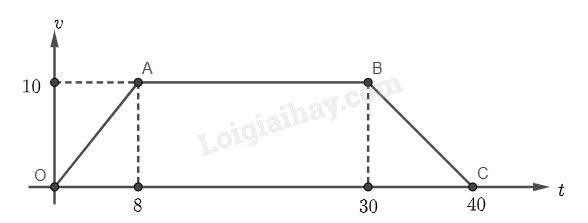
A. 400 m B. 350 m C. 310 m D. 200 m Phương pháp giải - Xem chi tiết Quãng đường đi được của ca nô trong khoảng thời gian 40 giây là \(s = \int\limits_0^{40} {v\left( t \right)dt} \). Viết phương trình hàm \(v\left( t \right)\), sau đó tính tích phân \(s = \int\limits_0^{40} {v\left( t \right)dt} \). Lời giải chi tiết Đồ thị hàm số \(v\left( t \right)\) được chia thành 3 đường thằng \(OA\), \(AB\), \(BC\) như hình dưới đây. Đường thẳng \(OA\) đi qua \(O\left( {0;0} \right)\) và \(A\left( {8;10} \right)\) nên phương trình đường thẳng \(OA\) là \(v = \frac{5}{4}t\). Đường thẳng \(AB\) đi qua \(A\left( {8;10} \right)\) và \(B\left( {30;10} \right)\) nên phương trình đường thẳng \(AB\) là \(v = 10\). Đường thẳng \(BC\) đi qua \(B\left( {30;10} \right)\) và \(C\left( {40;0} \right)\) nên phương trình đường thẳng \(BC\) là \(v = - t + 40\). Vậy \(v\left( t \right) = \left\{ \begin{array}{l}\frac{5}{4}t{\rm{ }}\left( {0 \le t \le 8} \right)\\10{\rm{ }}\left( {8 \le t \le 30} \right)\\ - t + 40{\rm{ }}\left( {30 \le t \le 40} \right)\end{array} \right.\). Do đó, quãng đường ca nô đi được trong 40 giây là \(s = \int\limits_0^{40} {v\left( t \right)dt} = \int\limits_0^8 {v\left( t \right)dt} + \int\limits_8^{30} {v\left( t \right)dt} + \int\limits_{30}^{40} {v\left( t \right)dt} = \int\limits_0^8 {\frac{5}{4}tdt} + \int\limits_8^{30} {10dt} + \int\limits_{30}^{40} {\left( { - t + 40} \right)dt} \) \( = \frac{5}{4}\left. {\left( {\frac{{{t^2}}}{2}} \right)} \right|_0^8 + 10\left. {\left( t \right)} \right|_8^{30} + \left. {\left( { - \frac{{{t^2}}}{2} + 40t} \right)} \right|_{30}^{40} = \frac{5}{4}.32 + 10.22 + 50 = 310\) (m). Đáp án đúng là C
|