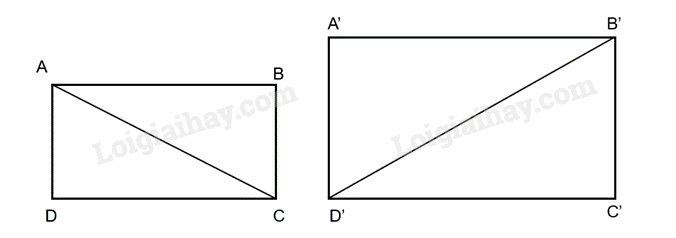
Giải bài 9.26 trang 103 SGK Toán 8 tập 2 - Kết nối tri thức

Đề bài

Cho hai hình chữ nhật ABCD và A'B'C'D' thỏa mãn AC=3AB, B′D′=3A′B′

a) Chứng minh rằng tam giác ABC đồng dạng với tam giác A'B'C'

b) Nếu A'B' = 2AB và diện tích hình chữ nhật ABCD là 2m² thì diện tích hình chữ nhật A'B'C'D' là bao nhiêu

Lời giải chi tiết

a) Có AC=3AB => \(\frac{{AB}}{{AC}} = \frac{1}{3}\)

- Có B′D′=3A′B′ => \(\frac{{A'B'}}{{B'D'}} = \frac{1}{3}\)

=> \(\frac{{AB}}{{A'B'}} = \frac{{AC}}{{B'D'}}\)

Xét tam giác vuông ABC (vuông tại A) và tam giác vuông A'B'D' (vuông tại C) có

=> \(\frac{{AB}}{{A'B'}} = \frac{{AC}}{{B'D'}}\)

=> ΔABC \( \backsim \) ΔC′D′B′ (1)

- Xét ΔC′D′B′ và ΔA′B′C′

Có B'C' chung, A′B′=C′D′, A′C′=B′D′ (hai hình chéo của chữ nhật)

=> ΔC′D′B′=ΔA′B′C′ (2)

Từ (1) và (2) chung =>ΔABC\( \backsim \) ΔA′B′C′

b) - Vì A′B′=2AB => \(\frac{{AB}}{{A'B'}} = \frac{1}{2}\)

mà ΔABC ∽ ΔA'B'C' => \(\frac{{AB}}{{A'B'}} = \frac{{AC}}{{A'C'}} = \frac{{BC}}{{B'C'}} = \frac{1}{2}\)

- Có diện tích ABCD là: AB.BC

  Có diện tích A'B'C'D' là: A′B′.B′C′

=> Xét tỉ lệ hai tam giác ABCD và A'B'C'D', có

\(\frac{{AB.BC}}{{A'B'.B'C'}} = \frac{{AB}}{{A'B'}}.\frac{{BC}}{{B'C'}} = \frac{1}{4}\)

=> \(S_{A′B′C′D′}=4S_{ABCD}\)

mà \(S_{ABCD}=2m^2\) => \(S_{A′B′C′D′}=8m^2\)