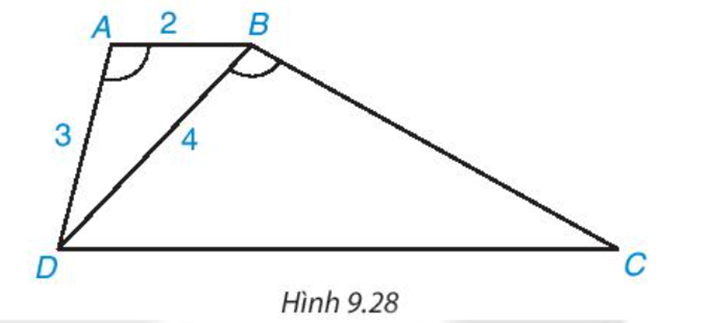
Giải bài 9.13 trang 92 SGK Toán 8 tập 2 - Kết nối tri thức

Đề bài

Cho hình thang ABCD (AB // CD) có \(\widehat {DAB} = \widehat {DBC}\)

a) Chứng minh rằng ΔABD ∽ ΔBDC 

b) Giả sử AB=2cm,AD=3cm,BD=4cm. Tính độ dài các cạnh BC và DC

Lời giải chi tiết

a) Có AB // CD Suy ra \(\widehat {AB{\rm{D}}} = \widehat {B{\rm{D}}C}\)

- Xét  ΔABD và ΔBDC

Có \(\widehat {AB{\rm{D}}} = \widehat {B{\rm{D}}C}{,^{}}\widehat {DAB} = \widehat {DBC}\)

Suy ra ΔABD ∽ ΔBDC (g.g)

b) Có \(\frac{{AB}}{{B{\rm{D}}}} = \frac{{12}}{{24}} = \frac{1}{2}\)

ΔABD ∽ ΔBDC với tỉ số \(\frac{1}{2}\)

Suy ra \(\frac{3}{{BC}} = \frac{4}{{DC}} = \frac{1}{2}\)

Suy ra BC=6 (cm)

     DC=8 (cm)