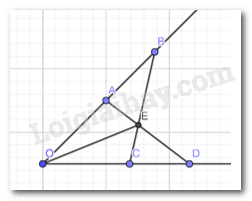
Giải bài 8 trang 58 SGK Toán 7 tập 2 - Chân trời sáng tạoCho góc xOy. Lấy hai điểm A, B thuộc tia Ox sao cho OA < OB. Lấy hai điểm C, D thuộc tia Oy sao cho OC = OA, OD = OB. Gọi E là giao điểm của AD và BC. Chứng minh rằng: a)AD = BC Tổng hợp đề thi học kì 2 lớp 7 tất cả các môn - Chân trời sáng tạo Toán - Văn - Anh - Khoa học tự nhiên... Đề bài Cho góc xOy. Lấy hai điểm A, B thuộc tia Ox sao cho OA < OB. Lấy hai điểm C, D thuộc tia Oy sao cho OC = OA, OD = OB. Gọi E là giao điểm của AD và BC. Chứng minh rằng: a) AD = BC b) c) OE là tia phân giác của góc xOy. Video hướng dẫn giải Phương pháp giải - Xem chi tiết Sử dụng các trường hợp bằng nhau của tam giác: c-c-c; c-g-c; g-c-g để chứng minh các tam giác bằng nhau rồi suy ra các cạnh tương ứng bằng nhau hoặc các góc tương ứng bằng nhau Lời giải chi tiết
a) Xét và , ta có : OD = OB chung OA = OC Suy ra (c-g-c ) Do đó (2 cạnh tương ứng ) b) Vì nên ( 2 góc tương ứng) Mà ( 2 góc kề bù) ( 2 góc kề bù) Do đó, Vì Mà suy ra Xét và , ta có:
Suy ra (g-c-g) c) Vì nên EB = ED ( 2 cạnh tương ứng) Xét và , ta có : EB = ED OB = OD OE chung Suy ra (c.c.c) Do đó ( 2 góc tương ứng) Dẫn đến OE là phân giác  Chia sẻ Bình luận
Tham Gia Group Dành Cho 2K12 Chia Sẻ, Trao Đổi Tài Liệu Miễn Phí
>> Học trực tuyến lớp 8 trên Tuyensinh247.com Đầy đủ khoá học các bộ sách (Kết nối tri thức với cuộc sống; Chân trời sáng tạo; Cánh diều). Cam kết giúp học sinh lớp 8 học tốt, hoàn trả học phí nếu học không hiệu quả.
|
