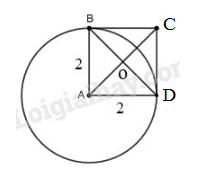
Bài 8 trang 157 SBT toán 9 tập 1

Đề bài

Cho hình vuông \(ABCD\), \(O\) là giao điểm của hai đường chéo, \(OA = \sqrt 2 \)cm. Vẽ đường tròn tâm \(A\) bán kính \(2cm.\)

Trong năm điểm \(A, B, C, D, O,\) điểm nào nằm trên đường tròn? 

Điểm nào nằm trong đường tròn? Điểm nào nằm ngoài đường tròn? 

Lời giải chi tiết

\(OA = \sqrt 2  < 2\) nên điểm \(O\) và \(A\) nằm trong \(( A; 2)\)

\(AB = 2\) nên điểm \(B\) nằm trên \((A ; 2)\)

\(AD = 2\) nên điểm \(D\) nằm trên \((A ; 2)\)

Xét tam giác ABC vuông tại B, theo định lý Pytago ta có: 

\(A{C^2} = A{B^2} + B{C^2} \)\(= {2^2} + {2^2} = 8 \Rightarrow AC = 2\sqrt 2 \)

Vì \(AC = 2\sqrt 2  > 2\) nên điểm \(C\) nằm ngoài \((A; 2).\)

HocTot.Nam.Name.Vn