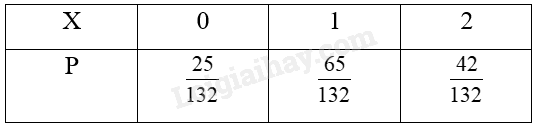
Giải bài 8 trang 12 Chuyên đề học tập Toán 12 - Cánh diềuCó hai nhóm học sinh. Nhóm thứ nhất có 5 nam và 6 nữ. Nhóm thứ hai có 5 nam và 7 nữ. Từ mỗi nhóm học sinh, ta chọn ngẫu nhiên 1 học sinh. Gọi X là số học sinh nữ trong số 2 học sinh được chọn ra. a) Lập bảng phân bố xác suất của biến ngẫu nhiên rời rạc X. b) Tính kì vọng, phương sai của X. Đề bài Có hai nhóm học sinh. Nhóm thứ nhất có 5 nam và 6 nữ. Nhóm thứ hai có 5 nam và 7 nữ. Từ mỗi nhóm học sinh, ta chọn ngẫu nhiên 1 học sinh. Gọi X là số học sinh nữ trong số 2 học sinh được chọn ra. a) Lập bảng phân bố xác suất của biến ngẫu nhiên rời rạc X. b) Tính kì vọng, phương sai của X. Phương pháp giải - Xem chi tiết a) Gọi \(X = 0;X = 1;X = 2\)lần lượt là biến cố: “không có HS nữ được chọn”; “ có 1 HS nữ trong 2 HS được chọn”; “chọn được 2 HS nữ.” Tính \(P(X = 0);P(X = 1);P(X = 2)\) Lập bảng phân bố xác suất. b) Áp dụng công thức: Kì vọng: \(E(X) = {x_1}{p_1} + {x_2}{p_2} + ... + {x_n}{p_n}\) Phương sai: \(V(X) = {({x_1} - \mu )^2}{p_1} + {({x_2} - \mu )^2}{p_2} + ... + {({x_n} - \mu )^2}{p_n}\) Lời giải chi tiết a) X là biến ngẫu nhiên rời rạc và nhận giá trị trong tập \(\left\{ {0;1;2} \right\}\) Ta có \(n(\Omega ) = C_{11}^1.C_{12}^1 = 132\) + Biến cố X=0 là biến cố :”Không có học sinh nữ được chọn.” Suy ra \(n(X = 0) = C_5^1.C_5^1 = 25 \Rightarrow P(X = 0) = \frac{{25}}{{132}}.\) + Biến cố X=1 là biến cố :”Có 1 học sinh nữ trong số 2 hs được chọn.” TH1: Nhóm 1 chọn được học sinh nữ, nhóm 2 chọn được học sinh nam Suy ra có \(C_6^1.C_5^1 = 30\) cách chọn TH2: Nhóm 1 chọn được học sinh nam, nhóm 2 chọn được học sinh nữ. Suy ra có \(C_5^1.C_7^1 = 35\) cách chọn Do đó \(P(X = 1) = \frac{{30 + 35}}{{132}} = \frac{{65}}{{132}}\) + Biến cố X=2 là biến cố :”Chọn được 2 HS nữ.” Suy ra \(n(X = 2) = C_6^1.C_7^1 = 42 \Rightarrow P(X = 2) = \frac{{42}}{{132}}.\) Bảng phân bố xác suất của X là:
b) Có: \(\begin{array}{l}E(X) = 0.\frac{{25}}{{132}} + 1.\frac{{65}}{{132}} + 2.\frac{{42}}{{132}} = \frac{{49}}{{132}}\\V(X) = {\left( {0 - \frac{{49}}{{132}}} \right)^2}.\frac{{25}}{{132}} + {\left( {1 - \frac{{49}}{{132}}} \right)^2}.\frac{{65}}{{132}} + {\left( {2 - \frac{{49}}{{132}}} \right)^2}.\frac{{42}}{{132}} \approx 0,49\end{array}\)  Chia sẻ Bình luận
Group Ôn Thi ĐGNL & ĐGTD Miễn Phí
|
