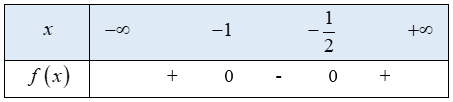
Giải bài 7 trang 61 SGK Toán 10 tập 1 – Cánh diều

Đề bài

Giải các bất phương trình sau:

a) $2{x^2} + 3x + 1 \ge 0$

b) $- 3{x^2} + x + 1 > 0$

c) $4{x^2} + 4x + 1 \ge 0$

d) $- 16{x^2} + 8x - 1 < 0$

e) $2{x^2} + x + 3 < 0$

g) $- 3{x^2} + 4x - 5 < 0$

Lời giải chi tiết

a) $2{x^2} + 3x + 1 \ge 0$

Tam thức bậc hai $f\left( x \right) = 2{x^2} + 3x + 1$ có 2 nghiệm phân biệt $x =  - 1,x = \frac{{ - 1}}{2}$

hệ số $a = 2 > 0$

Ta có bảng xét dấu f(x) như sau:

Từ bảng xét dấu ta thấy $f\left( x \right) \ge 0 \Leftrightarrow \left[ \begin{array}{l}x \le  - 1\\x \ge  - \frac{1}{2}\end{array} \right.$

Vậy tập nghiệm của bất phương trình là $\left( { - \infty ; - 1} \right] \cup \left[ { - \frac{1}{2}; + \infty } \right)$

b) $- 3{x^2} + x + 1 > 0$

Tam thức bậc hai $f\left( x \right) =  - 3{x^2} + x + 1$ có 2 nghiệm phân biệt $x = \frac{{1 - \sqrt {13} }}{6},x = \frac{{1 + \sqrt {13} }}{6}$

Hệ số $a =  - 3 < 0$

Ta có bảng xét dấu f(x) như sau:

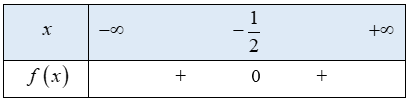
Từ bảng xét dấu ta thấy $f\left( x \right) > 0$$\Leftrightarrow \frac{{1 - \sqrt {13} }}{6} < x < \frac{{1 + \sqrt {13} }}{6}$

Vậy tập nghiệm của bất phương trình là $\left( {\frac{{1 - \sqrt {13} }}{6};\frac{{1 + \sqrt {13} }}{6}} \right)$

c) $4{x^2} + 4x + 1 \ge 0$

Tam thức bậc hai $f\left( x \right) = 4{x^2} + 4x + 1$ có nghiệm duy nhất $x = \frac{{ - 1}}{2}$

hệ số $a = 4 > 0$

Ta có bảng xét dấu f(x) như sau:

Từ bảng xét dấu ta thấy $f\left( x \right) \ge 0 \Leftrightarrow x \in \mathbb{R}$

Vậy tập nghiệm của bất phương trình là $\mathbb{R}$

d) $- 16{x^2} + 8x - 1 < 0$

Tam thức bậc hai $f\left( x \right) =  - 16{x^2} + 8x - 1$ có nghiệm duy nhất $x = \frac{1}{4}$

hệ số $a =  - 16 < 0$

Ta có bảng xét dấu f(x) như sau:

Từ bảng xét dấu ta thấy $f\left( x \right) < 0 \Leftrightarrow x \ne \frac{1}{4}$

Vậy tập nghiệm của bất phương trình là $\mathbb{R}\backslash \left\{ {\frac{1}{4}} \right\}$

e) $2{x^2} + x + 3 < 0$

Ta có $\Delta  = {1^2} - 4.2.3 =  - 23 < 0$ và có $a = 2 > 0$

Sử dụng định lí về dấu của tam thức bậc hai, ta thấy tập hợp những giá trị của x sao cho $2{x^2} + x + 3$ mang dấu “-” là $\emptyset$

Vậy tập nghiệm của bất phương trình $2{x^2} + x + 3 < 0$ là $\emptyset$

g) $- 3{x^2} + 4x - 5 < 0$

Tam thức bậc hai $f\left( x \right) =  - 3{x^2} + 4x - 5$ có $\Delta ' = {2^2} - \left( { - 3} \right).\left( { - 5} \right) =  - 11 < 0$ và có $a =  - 3 < 0$

Sử dụng định lí về dấu của tam thức bậc hai, ta thấy tập hợp những giá trị của x sao cho $- 3{x^2} + 4x - 5$ mang dấu “-” là $\mathbb{R}$

Vậy tập nghiệm của bất phương trình $- 3{x^2} + 4x - 5 < 0$ là $\mathbb{R}$