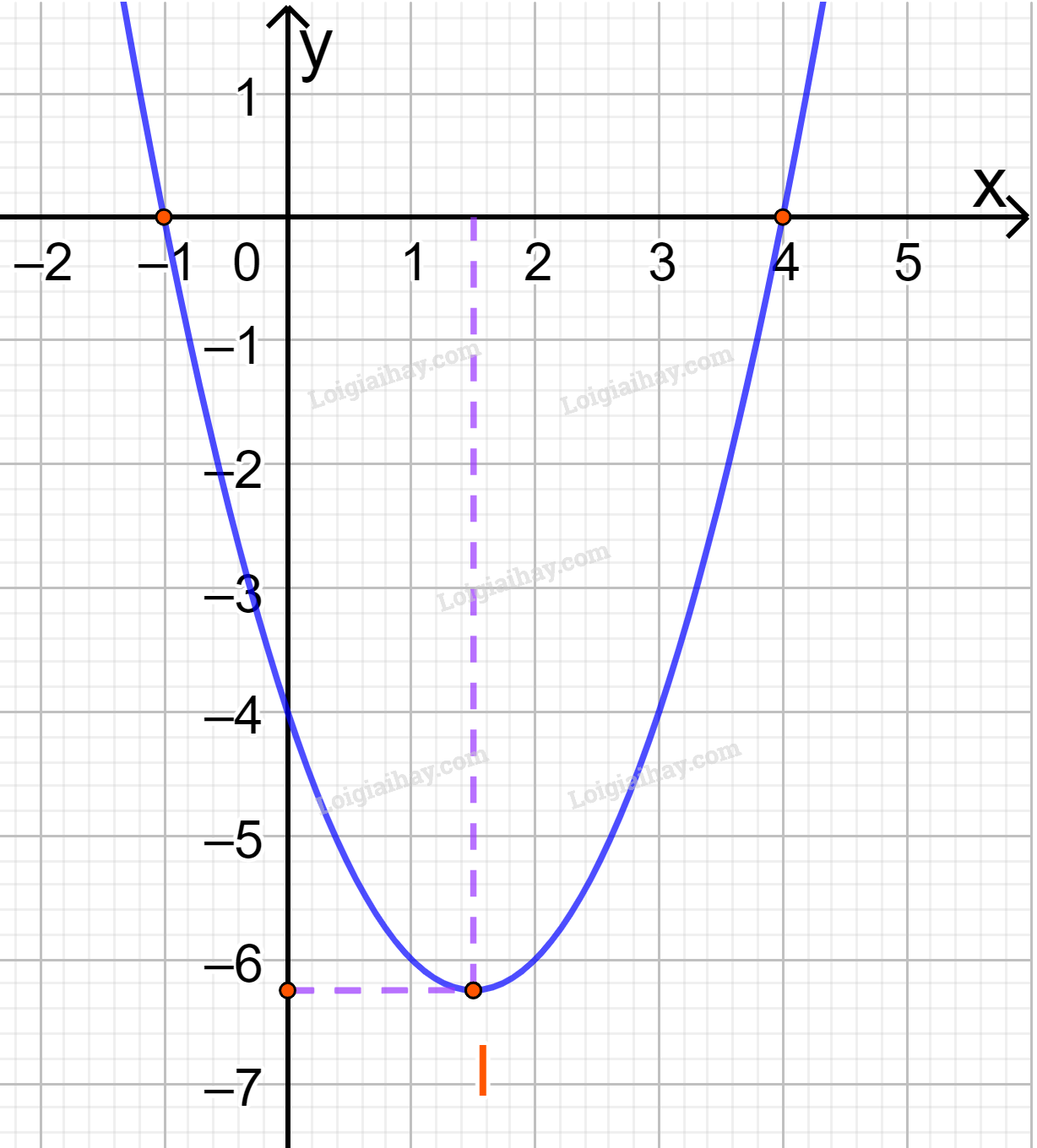
Giải bài 5 trang 61 SGK Toán 10 tập 1 – Cánh diềuVẽ đồ thị của mỗi hàm số sau Tổng hợp đề thi học kì 2 lớp 10 tất cả các môn - Cánh diều Toán - Văn - Anh - Lí - Hóa - Sinh - Sử - Địa... Đề bài Vẽ đồ thị của mỗi hàm số sau: a) y=x2−3x−4 b) y=x2+4x+4 c) y=−x2+2x−2 Phương pháp giải - Xem chi tiết Bước 1: Xác định tọa độ đỉnh (−b2a;−Δ4a) Bước 2: Vẽ trục đối xứng x=−b2a Bước 3: Xác định một số điểm đặc biệt, chẳng hạn giao điểm với trục tung (0;c) và trục hoành (nếu có), điểm đối xứng với điểm (0;c) qua trục x=−b2a. Bước 4: Vẽ đường parabol đi qua các điểm đã xác định ta nhận được đồ thị hàm số y=ax2+bx+c. Lời giải chi tiết a) y=x2−3x−4 Đồ thị hàm số có đỉnh I(32;−254) Trục đối xứng là x=32 Giao điểm của parabol với trục tung là (0;-4) Giao điểm của parabol với trục hoành là (-1;0) và (4;0) Điểm đối xứng với điểm (0;-4) qua trục đối xứng x=32 là (3;-4) Vẽ parabol đi qua các điểm được xác định ở trên, ta nhận được đồ thị hàm số:
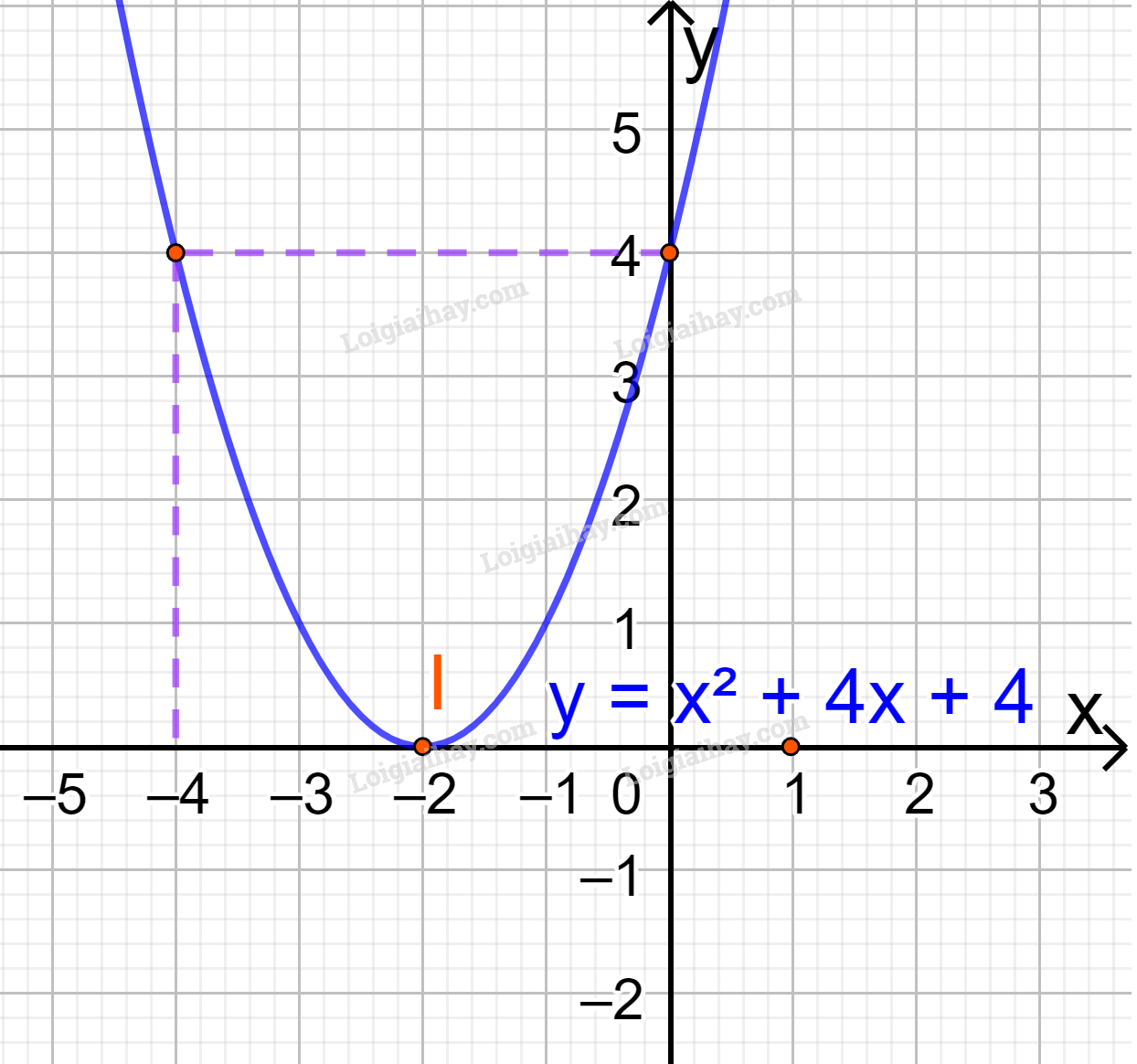
b) y=x2+4x+4 Đồ thị hàm số có đỉnh I(−2;0) Trục đối xứng là x=−2 Giao điểm của parabol với trục tung là (0;4) Giao điểm của parabol với trục hoành là I(-2;0) Điểm đối xứng với điểm (0;4) qua trục đối xứng x=−2 là (-4;4) Vẽ parabol đi qua các điểm được xác định ở trên, ta nhận được đồ thị hàm số:
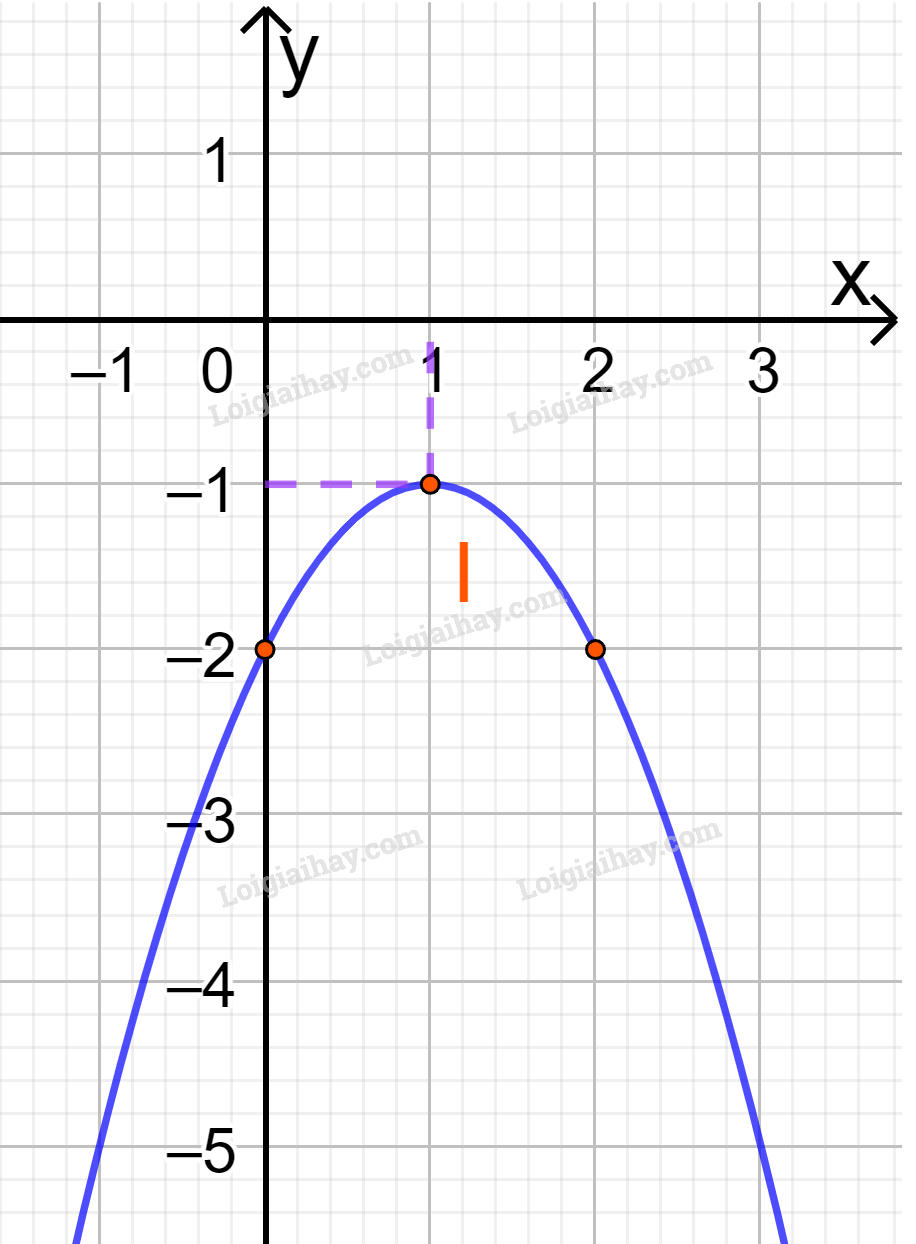
c) y=−x2+2x−2 Đồ thị hàm số có đỉnh I(1;−1) Trục đối xứng là x=1 Giao điểm của parabol với trục tung là (0;-2) Điểm đối xứng với điểm (0;-2) qua trục đối xứng x=1 là (2;-2) Vẽ parabol đi qua các điểm được xác định ở trên, ta nhận được đồ thị hàm số:
>> 2K9 Học trực tuyến - Định hướng luyện thi TN THPT, ĐGNL, ĐGTD ngay từ lớp 11 (Click để xem ngay) cùng thầy cô giáo giỏi trên Tuyensinh247.com. Bứt phá điểm 9,10 chỉ sau 3 tháng, tiếp cận sớm các kì thi.
|