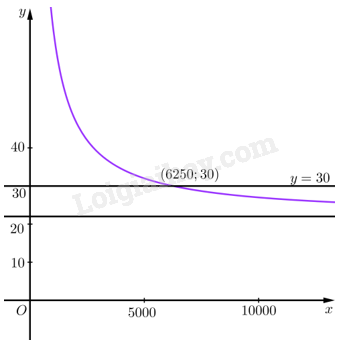
Giải bài 7 trang 37 sách bài tập toán 12 - Chân trời sáng tạoMột chủ nhà hàng kinh doanh phần ăn đồng giá có chiến lược kinh doanh nhur sau: • Phí cố định được ước tính trong một năm là 50000 nghìn đồng. • Chi phí một phần ăn ước tính khoảng 22 nghìn đồng. • Giá niêm yết trên thực đơn là 30 nghìn đồng. Trong bài này, giả định rằng tất cả các phần ăn chế biến sẵn đều được bán hết và kí hiệu (x) là số phần ăn phục vụ trong một năm, giả sử (x) thuộc khoảng (left[ {5000;25000} right]). a) Gọi (Cleft( x right)) là tổng chi phí hằng năm ch Tổng hợp đề thi học kì 2 lớp 12 tất cả các môn - Chân trời sáng tạo Toán - Văn - Anh - Hoá - Sinh - Sử - Địa Đề bài Một chủ nhà hàng kinh doanh phần ăn đồng giá có chiến lược kinh doanh nhur sau: • Phí cố định được ước tính trong một năm là 50000 nghìn đồng. • Chi phí một phần ăn ước tính khoảng 22 nghìn đồng. • Giá niêm yết trên thực đơn là 30 nghìn đồng. Trong bài này, giả định rằng tất cả các phần ăn chế biến sẵn đều được bán hết và kí hiệu x là số phần ăn phục vụ trong một năm, giả sử x thuộc khoảng [5000;25000]. a) Gọi C(x) là tổng chi phí hằng năm cho x phần ăn này. Xác định C(x). b) Chứng tỏ rằng giá thành của một phần ăn cho bởi biểu thức D(x)=22+50000x (nghìn đồng). c) Sử dụng đồ thị, hãy xác định điểm hoà vốn của nhà hàng, tức là số lượng phần ăn tối thiểu phải được phục vụ hằng năm để hoạt động của nhà hàng tạo ra lợi nhuận. Hãy chứng minh điều đó. d) Chứng minh rằng tổng lợi nhuận hằng năm cho x phần ăn được biểu thị bởi: L(x)=8x−50000 (nghìn đồng). e) Mục tiêu của chủ nhà hàng là tạo ra lợi nhuận ít nhất là 120000 nghìn đồng mỗi năm. Biết rằng nhà hàng mở cửa 300 ngày một năm, hỏi trung bình mỗi ngày nhà hàng phải phục vụ ít nhất bao nhiêu phần ăn để đạt được mục tiêu trên? Phương pháp giải - Xem chi tiết ‒ Biểu diễn các đại lượng chưa biết qua các đại lượng đã biết. ‒ Để xác định điểm hoà vốn của nhà hàng, ta tìm giao điểm của đồ thị hàm số D(x) và đường thẳng y=30. ‒ Giải bất phương trình L(x)≥120000 để xác định số phần ăn trung bình nhà hàng phải phục vụ mỗi ngày để đạt được mục tiêu. Lời giải chi tiết a) Tổng chi phí hằng năm cho x phần ăn là: C(x)=22x+50000 (nghìn đồng). b) Giá thành của một phần ăn là: D(x)=22x+50000x=22+50000x (nghìn đồng). c) Xét hàm số D(x)=22+50000x. Ta có: D′(x)=−50000x2<0 Khi đó ta có đồ thị hàm số D(x) và đường thẳng y=30 như sau:
Quan sát đồ thị của hai hàm số, ta thấy giao điểm của đồ thị hàm số D(x) và đường thẳng y=30 là điểm có toạ độ (6250;30). Nghĩa là khi phục vụ được tối thiểu 6250 phần ăn thì chi phí một phần ăn đúng bằng tiền bán một phần ăn (là 30 nghìn đồng). Đồ thị cũng cho thấy rằng nếu phục vụ được ít hơn 6250 phần ăn thì chi phí cho 1 phần ăn cao hơn giá bán 1 phần ăn, nghĩa là nhà hàng sẽ lỗ. Như vậy điểm hoà vốn là 6250. d) L(x)=30x−(22x+50000)=8x−50000 (nghìn đồng). e) Để đạt mục tiêu lợi nhuận hằng năm ít nhất là 120000 nghìn đồng thì số phần ăn cần bán được phải thoả mãn bất phương trình sau: L(x)≥120000⇔8x−50000≥120000⇔x≥21250. Vậy nhà hàng cần phục vụ được tối thiểu 21250 phần ăn thì mới có lợi nhuận như mong muốn. Do nhà hàng mở cửa 300 ngày một năm nên trung bình mỗi ngày nhà hàng cần phục vụ được khoảng 21250:300≈70,8 phần ăn. Vậy để đạt mục tiêu, trung bình mỗi ngày nhà hàng cần phục vụ ít nhất 71 phần ăn.
>> 2K8 Chú ý! Lộ Trình Sun 2026 - 3IN1 - 1 lộ trình ôn 3 kì thi (Luyện thi 26+ TN THPT, 90+ ĐGNL HN, 900+ ĐGNL HCM, 70+ ĐGTD - Click xem ngay) tại Tuyensinh247.com.Đầy đủ theo 3 đầu sách, Thầy Cô giáo giỏi, luyện thi theo 3 giai đoạn: Nền tảng lớp 12, Luyện thi chuyên sâu, Luyện đề đủ dạng đáp ứng mọi kì thi.
|