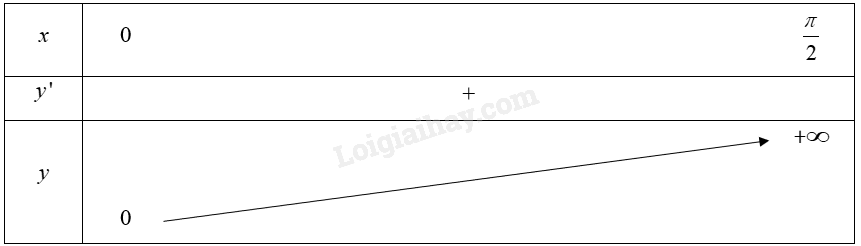
Giải bài 7 trang 11 sách bài tập toán 12 - Chân trời sáng tạo

Chứng minh rằng a) (tan x > x) với mọi (x in left( {0;frac{pi }{2}} right)); b) (ln x le x - 1) với mọi (x > 0).

Tổng hợp đề thi học kì 2 lớp 12 tất cả các môn - Chân trời sáng tạo

Toán - Văn - Anh - Hoá - Sinh - Sử - Địa

Đề bài

Chứng minh rằng

a) $\tan x > x$ với mọi $x \in \left( {0;\frac{\pi }{2}} \right)$ ;

b) $\ln x \le x - 1$ với mọi $x > 0$ .

Phương pháp giải - Xem chi tiết

Đưa về xét hàm số, lập bảng biến thiên của hàm số trên khoảng.

Quảng cáo

Lời giải chi tiết

a) Đặt $f\left( x \right) = \tan x - x$ với mọi $x \in \left( {0;\frac{\pi }{2}} \right)$ .

Ta có $f'\left( x \right) = \frac{1}{{{{\cos }^2}x}} - 1 = \frac{{1 - {{\cos }^2}x}}{{{{\cos }^2}x}} = \frac{{{{\sin }^2}x}}{{{{\cos }^2}x}} = {\tan ^2}x > 0$ với mọi $x \in \left( {0;\frac{\pi }{2}} \right)$ .

Bảng biến thiên:

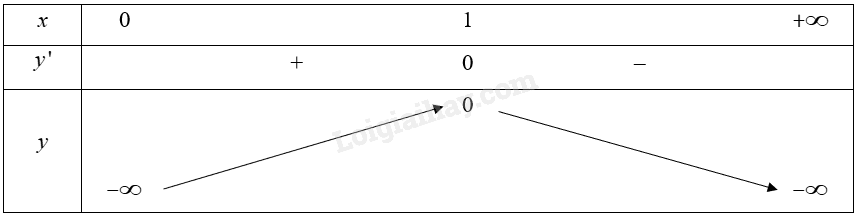
Do đó $f'\left( x \right) > f\left( 0 \right) = 0$ với mọi $x \in \left( {0;\frac{\pi }{2}} \right)$ .

Suy ra $\tan x - x > 0$ với mọi $x \in \left( {0;\frac{\pi }{2}} \right)$ .

Vậy $\tan x > x$ với mọi $x \in \left( {0;\frac{\pi }{2}} \right)$ .

b) Đặt $f\left( x \right) = \ln x - x + 1$ với mọi $x > 0$ .

Ta có $f'\left( x \right) = \frac{1}{x} - 1 = \frac{{1 - x}}{x};f'\left( x \right) = 0 \Leftrightarrow x = 1$ .

Bảng biến thiên:

Hàm số $y = f\left( x \right)$ đồng biến trên khoảng $\left( {0;1} \right)$ , nghịch biến trên khoảng $\left( {1; + \infty } \right)$ .

Do đó $f\left( x \right) \le f\left( 1 \right) = 0$ với mọi $x > 0$ .

Suy ra $\ln x - x + 1 \le 0$ với mọi $x > 0$ .

Vậy $\ln x \le x - 1$ với mọi $x > 0$ .

Chia sẻ

Bình luận

Bình chọn:

4.9 trên 7 phiếu

Giải bài 8 trang 11 sách bài tập toán 12 - Chân trời sáng tạo
Chứng minh rằng: a) Phương trình ${x^3} + 5{x^2} - 8{\rm{x}} + 4 = 0$ có duy nhất một nghiệm. b) Phương trình $- {x^3} + 3{x^2} + 24x - 1 = 0$ có ba nghiệm phân biệt.
Giải bài 9 trang 11 sách bài tập toán 12 - Chân trời sáng tạo
Tìm $m$ để phương trình $\frac{{{x^2} + x + 4}}{{x + 1}} = m$ có hai nghiệm phân biệt.
Giải bài 10 trang 11 sách bài tập toán 12 - Chân trời sáng tạo
Một chất điểm chuyển động lên, xuống theo phương thẳng đứng. Độ cao $h\left( t \right)$ của chất điểm tại thời điểm $t$ (giây) được cho bởi công thức $h\left( t \right) = \frac{1}{3}{t^3} - 4{t^2} + 12t + 1$ với $0 \le t \le 8$ . a) Viết công thức tính vận tốc của chất điểm. b) Trong khoảng thời gian nào chất điểm chuyển động lên, trong thời gian nào chất điểm chuyển động đi xuống?
Giải bài 11 trang 11 sách bài tập toán 12 - Chân trời sáng tạo
Độ cao (tính bằng mét) của tàu lượn siêu tốc so với mặt đất sau $t$ (giây) $\left( {0 \le t \le 20} \right)$ từ lúc bắt đầu được cho bởi công thức $h\left( t \right) = - \frac{4}{{255}}{t^3} + \frac{{49}}{{85}}{t^2} - \frac{{98}}{{17}}t + 20$ . Trong khoảng thời gian nào tàu lượn đi xuống, trong khoảng thời gian nào tàu lượn đi lên?
Giải bài 12 trang 12 sách bài tập toán 12 - Chân trời sáng tạo
Cho điểm $A$ di động trên nửa đường tròn tâm $O$ đường kính $MN = 20{\rm{ }}cm,\widehat {MOA} = \alpha$ với $0 \le \alpha \le \pi$ . Lấy điểm $B$ thuộc nửa đường tròn và $C,D$ thuộc đường kính $MN$ được xác định sao cho $ABCD$ là hình chữ nhật. Khi $A$ di động từ trái sang phải, trong các khoảng nào của $\alpha$ thì diện tích của hình chữ nhật $ABCD$ tăng, trong các khoảng nào của $\alpha$ thì diện tích của hình chữ nhật $ABCD$ giảm?

Luyện Bài Tập Trắc nghiệm Toán 12 - Chân trời sáng tạo - Xem ngay

Báo lỗi - Góp ý

Group 2K8 ôn Thi ĐGNL & ĐGTD Miễn Phí

>> 2K8 Chú ý! Lộ Trình Sun 2026 - 3IN1 - 1 lộ trình ôn 3 kì thi (Luyện thi 26+ TN THPT, 90+ ĐGNL HN, 900+ ĐGNL HCM, 70+ ĐGTD - Click xem ngay) tại Tuyensinh247.com.Đầy đủ theo 3 đầu sách, Thầy Cô giáo giỏi, luyện thi theo 3 giai đoạn: Nền tảng lớp 12, Luyện thi chuyên sâu, Luyện đề đủ dạng đáp ứng mọi kì thi.