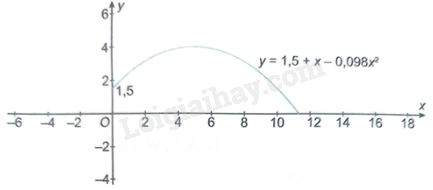
Giải bài 6.15 trang 10 sách bài tập toán 9 - Kết nối tri thức tập 2Quỹ đạo chuyển động của một quả bóng được cho bởi công thức (y = 1,5 + x - 0,098{x^2}), trong đó y (mét) là độ cao của quả bóng so với mặt đất và x (mét) là khoảng cách theo phương ngang từ vị trí của quả bóng đến vị trí ném (xem hình bên). Tính khoảng cách theo phương ngang từ vị trí ném bóng đến vị trí quả bóng chạm đất. Tổng hợp Đề thi vào 10 có đáp án và lời giải Toán - Văn - Anh Đề bài Quỹ đạo chuyển động của một quả bóng được cho bởi công thức \(y = 1,5 + x - 0,098{x^2}\), trong đó y (mét) là độ cao của quả bóng so với mặt đất và x (mét) là khoảng cách theo phương ngang từ vị trí của quả bóng đến vị trí ném (xem hình bên). Tính khoảng cách theo phương ngang từ vị trí ném bóng đến vị trí quả bóng chạm đất.
Phương pháp giải - Xem chi tiết + Vật chạm đất khi \(y = 0\), tức là \(1,5 + x - 0,098{x^2} = 0\). + Giải phương trình vừa tìm được, lấy giá trị x dương, từ đó rút ra kết luận. Lời giải chi tiết Vật chạm đất khi \(y = 0\), tức là \(1,5 + x - 0,098{x^2} = 0\) Vì \(\Delta = {1^2} - 4.1,5.\left( { - 0,098} \right) = 1,588 > 0\). Vì \(x > 0\) nên \(x = \frac{{ - 1 - \sqrt {1,588} }}{{2.\left( { - 0,098} \right)}} \approx 11,53\). Vậy khoảng cách theo phương ngang từ vị trí ném bóng đến vị trí bóng chạm đất là khoảng 11,53m.  Chia sẻ Bình luận
Tham Gia Group 2K10 Ôn Thi Vào Lớp 10 Miễn Phí
>> Học trực tuyến lớp 9 và Lộ trình UP10 trên Tuyensinh247.com Đầy đủ khoá học các bộ sách: Kết nối tri thức với cuộc sống; Chân trời sáng tạo; Cánh diều. Lộ trình học tập 3 giai đoạn: Học nền tảng lớp 9, Ôn thi vào lớp 10, Luyện Đề. Bứt phá điểm lớp 9, thi vào lớp 10 kết quả cao. Hoàn trả học phí nếu học không hiệu quả.
|
