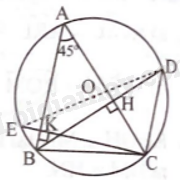
Giải bài 6 trang 93 sách bài tập toán 9 - Chân trời sáng tạo tập 1Cho tam giác nhọn ABC có (widehat {BAC} = {45^o}) và có các đỉnh nằm trên đường tròn (O). Các đường cao BH, CK cắt đường tròn (O) tại D, E. Chứng minh ba điểm D, O, E thẳng hàng. Đề bài Cho tam giác nhọn ABC có ^BAC=45o và có các đỉnh nằm trên đường tròn (O). Các đường cao BH, CK cắt đường tròn (O) tại D, E. Chứng minh ba điểm D, O, E thẳng hàng. Phương pháp giải - Xem chi tiết Dựa vào các góc nội tiếp cùng chắn một cung thì bằng nhau để chứng minh DE là đường kính. Lời giải chi tiết
Ta có BH⊥AC nên tam giác ABH vuông tại H. Mà ^BAH=45o nên ^ABH=45o. Mặt khác ^ABD=^ACD (góc nội tiếp cùng chắn ⌢AD) nên ^ACD=45o (1) Ta có CK⊥AB nên tam giác ACK vuông tại K. Mà ^CAK=45o nên ^ACK=45o (2) Từ (1) và (2) suy ra ^DCE=90o nên DE là đường kính. Vậy ba điểm D, O, E thẳng hàng.  Chia sẻ Bình luận
Tham Gia Group Dành Cho Lớp 9 - Ôn Thi Vào Lớp 10 Miễn Phí
|
