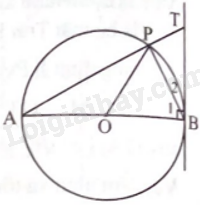
Giải bài 5 trang 93 sách bài tập toán 9 - Chân trời sáng tạo tập 1Cho đường tròn (O) đường kính AB và một dây cung AP. Tia AP cắt tiếp tuyến tại B của đường tròn (O) tại T. Chứng minh rằng: a) (widehat {AOP} = 2widehat {ATB}) b) (widehat {APO} = widehat {PBT}) Đề bài Cho đường tròn (O) đường kính AB và một dây cung AP. Tia AP cắt tiếp tuyến tại B của đường tròn (O) tại T. Chứng minh rằng: a) \(\widehat {AOP} = 2\widehat {ATB}\) b) \(\widehat {APO} = \widehat {PBT}\) Phương pháp giải - Xem chi tiết Dựa vào góc nội tiếp bằng nửa góc ở tâm cùng chắn một cung. Lời giải chi tiết
a) Ta có \(\widehat {ATB} = \widehat {{B_1}}\) (cùng phụ với \(\widehat {{B_2}}\)). Mà \(\widehat {{B_1}} = \frac{1}{2}\widehat {AOP}\) (góc nội tiếp và góc ở tâm cùng chắn cung \(\overset\frown{AP}\)) nên \(\widehat {ATB} = \frac{1}{2}\widehat {AOP}\) hay \(\widehat {AOP} = 2\widehat {ATB}\). b) AO = PO nên tam giác AOP cân tại O suy ra \(\widehat {PAO} = \widehat {APO}\). Mà \(\widehat {PAO} = \widehat {PBT}\) (cùng phụ với \(\widehat {{B_1}})\), suy ra \(\widehat {APO} = \widehat {PBT}\).
|