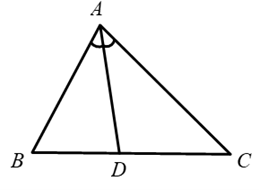
Giải bài 53 trang 100 SBT toán 10 - Cánh diềuCho tam giác ABC, kẻ phân giác AD. Đặt AB = c, AC = b. Chứng minh: Tổng hợp đề thi học kì 2 lớp 10 tất cả các môn - Cánh diều Toán - Văn - Anh - Lí - Hóa - Sinh - Sử - Địa... Đề bài Cho tam giác ABC, kẻ phân giác AD. Đặt AB = c, AC = b. Chứng minh: \(b\overrightarrow {DB} + c\overrightarrow {DC} = \overrightarrow 0 \) (*) Phương pháp giải - Xem chi tiết Bước 1: Biểu diễn độ dài DB (hoặc DC) theo DC (hoặc DB) và xác định hướng các vectơ tương ứng Bước 2: Sử dụng định lí đường phân giác trong tam giác để biến đổi tỉ số độ dài \(\frac{{DB}}{{DC}}\) Bước 3: Biến đổi đẳng thức ở bước 1 rồi kết luận Lời giải chi tiết
Ta có: \(DB = \frac{{DB}}{{DC}}.DC\) mà \(\overrightarrow {DB} \) và \(\overrightarrow {DC} \) ngược hướng \( \Rightarrow \overrightarrow {DB} = - \frac{{DB}}{{DC}}.\overrightarrow {DC} \)(1) Theo giả thiết, AD là đường phân giác của ∆ABC \( \Rightarrow \frac{{AB}}{{AC}} = \frac{{DB}}{{DC}} = \frac{c}{b}\) (2) Từ (1) và (2) suy ra \(\overrightarrow {DB} = - \frac{c}{b}.\overrightarrow {DC} \Leftrightarrow b\overrightarrow {DB} = - c\overrightarrow {DC} \Leftrightarrow b\overrightarrow {DB} + c\overrightarrow {DC} = \overrightarrow 0 \) (ĐPCM)
 Chia sẻ Bình luận
2k8 Tham gia ngay group chia sẻ, trao đổi tài liệu học tập miễn phí
|
