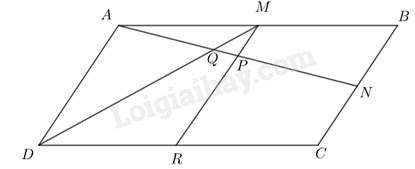
Giải bài 5 trang 94 SGK Toán 8 – Cánh diều

Đề bài

Cho hình bình hành ABCD. Gọi M, N, P lần lượt là trung điểm của các đoạn thẳng AB, BC, AN và Q là giao điểm của AN và DM. Chứng minh:

a) $MP\parallel AD,\,\,MP = \frac{1}{4}AD$

b) $AQ = \frac{2}{5}AN$

c) Gọi R là trung điểm của CD. Chứng minh ba điểm M, P, R thẳng hàng và $PR = \frac{3}{4}AD$.

Lời giải chi tiết

Vì M và P lần lượt là trung điểm của AB và AN nên MP là đường trung bình của tam giác ABN.

$\Rightarrow MP\parallel BN$ hay $MP\parallel BC$.

Mà ABCD là hình bình hành nên $AD\parallel BC$

$\Rightarrow MP\parallel AD$

Ta có: $MP = \frac{1}{2}NB$

Mà N là trung điểm BC nên $NB = \frac{1}{2}BC$

$\Rightarrow MP = \frac{1}{4}BC \Rightarrow MP = \frac{1}{4}AD$

b) Vì $MP\parallel AD$ nên $\frac{{MP}}{{AD}} = \frac{{QP}}{{AQ}}$ (hệ quả của định lý Thales)

$\Rightarrow \frac{{QP}}{{AQ}} = \frac{1}{4} \Rightarrow AQ = 4QP\,\,\left( 1 \right)$

Ta có: $QP = AP - AQ = \frac{1}{2}AN - AQ$ (P là trung điểm AN)

Thay vào (1) ta được $AQ = 4.\left( {\frac{1}{2}AN - AQ} \right)$

$\Rightarrow AQ = 2AN - 4AQ \Rightarrow 5AQ = 2AN \Rightarrow AQ = \frac{2}{5}AN$ (đpcm)

c) Vì M và R lần lượt là trung điểm của AB và CD nên $MR\parallel AD,\,\,MR = AD$

Mà ta đã chứng minh $MP\parallel AD$ nên ba điểm M, P, R thẳng hàng.

Theo câu a) ta có $MP = \frac{1}{4}AD \Rightarrow MP = \frac{1}{4}MR$

$\Rightarrow PR = \frac{3}{4}MR \Rightarrow PR = \frac{3}{4}AD$.