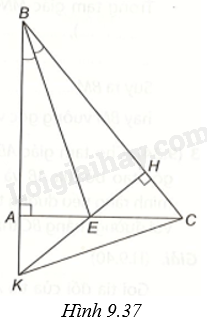
Giải bài 5 trang 83 vở thực hành Toán 7 tập 2

Đề bài

Cho $\Delta ABC$ vuông tại A. Tia phân giác của $\widehat {ABC}$ cắt AC tại E. Từ E kẻ $EH \bot BC$ tại H và EH cắt AB tại K.

a) Chứng minh $AE = EH$.

b) So sánh độ dài hai cạnh AE và EC.

c) Chứng minh BE là đường trung trực của AH.

d) Chứng minh $\Delta KBC$ là tam giác cân.

Lời giải chi tiết

(H.9.37)

a) Xét $\Delta ABE$ và $\Delta HBE$ có: BE chung, $\widehat {ABE} = \widehat {EBH}$, $\widehat {BAE} = \widehat {BHE} = {90^o}$

Do đó, $\Delta ABE = \Delta HBE$ (cạnh huyền – góc nhọn)

Suy ra $AE = EH$ (hai cạnh tương ứng).

b) Trong tam giác vuông EHC, ta có EC là cạnh huyền nên $EH < EC$, mà $AE = EH$(cmt) nên $AE < EC$.

c) Từ $\Delta ABE = \Delta HBE$, suy ra $AB = HB$ (hai cạnh tương ứng), suy ra tam giác ABH cân tại B có BE là đường phân giác nên BE cũng là đường trung trực của AH.

d) Tam giác KBC có hai đường cao CA và KH cắt nhau tại E nên E là trực tâm của tam giác KBC, do đó BE là đường cao của tam giác KBC.

Mặt khác có BE là đường phân giác của tam giác KBC nên BE vừa là đường cao vừa là đường phân giác của tam giác KBC, suy ra tam giác KBC cân tại B.