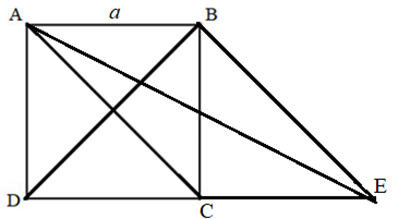
Giải bài 42 trang 92 SBT toán 10 - Cánh diềuCho hình vuông ABCD cạnh a. Tính \(\left| {\overrightarrow {AB} + \overrightarrow {AC} } \right|\) Tổng hợp đề thi học kì 1 lớp 10 tất cả các môn - Cánh diều Toán - Văn - Anh - Lí - Hóa - Sinh - Sử - Địa... Đề bài Cho hình vuông ABCD cạnh a. Tính \(\left| {\overrightarrow {AB} + \overrightarrow {AC} } \right|\) Phương pháp giải - Xem chi tiết Dựng hình bình hành ABEC rồi biến đổi giả thiết để tính độ dài \(\left| {\overrightarrow {AB} + \overrightarrow {AC} } \right|\) Lời giải chi tiết Dựng hình bình hành ABEC. Khi đó \(\overrightarrow {AB} + \overrightarrow {AC} = \overrightarrow {AE} \) Ta có: \(\left| {\overrightarrow {AB} + \overrightarrow {AC} } \right| = \left| {\overrightarrow {AE} } \right| = AE\) Xét tam giác ADE vuông tại D có \(AE = \sqrt {A{D^2} + D{E^2}} = \sqrt {{a^2} + {{(2a)}^2}} = \sqrt {5{a^2}} = a\sqrt 5 \) Vậy \(\left| {\overrightarrow {AB} + \overrightarrow {AC} } \right| = AE = a\sqrt 5 \)
|