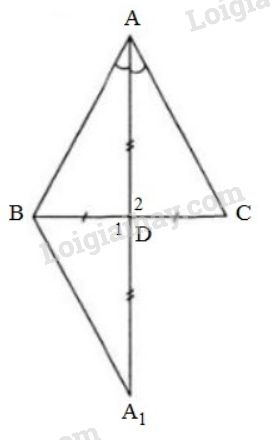
Bài 41 trang 88 Vở bài tập toán 7 tập 2Giải bài 41 trang 88 VBT toán 7 tập 2. Chứng minh định lí : Nếu tam giác có một đường trung tuyến đồng thời là đường phân giác thì tam giác đó là ... Đề bài Chứng minh định lí: Nếu tam giác có một đường trung tuyến đồng thời là đường phân giác thì tam giác đó là tam giác cân. Phương pháp giải - Xem chi tiết Gợi ý : Kéo dài AD một đoạn DA1 sao cho DA1=AD. Lời giải chi tiết
Giả sử tam giác ABC có đường trung tuyến AD đồng thời là đường phân giác. Trên tia AD lấy điểm A1 sao cho DA1=AD. Ta sẽ chứng minh tam giác ABC cân tại A. Xét hai tam giác ADC và A1DB. Ta có DC=DB (vì AD là đường trung tuyến của tam giác ABC), AD=DA1 (theo cách lấy điểm A1), ^BDA1=^CDA (hai góc đối đỉnh). Vậy ∆ADC=∆A1DB (c.g.c). Suy ra ^DAC=^DA1B (1), AC=BA1 (2). Xét tam giác BAA1. Ta có ^BAA1=^BA1A (vì theo (1) ^BA1D=^DAC và do AD là đường phân giác nên ^DAC=^BAA1). Suy ra tam giác BAA1 cân tại B, do đó AB=A1B (3) Từ (2) và (3) suy ra AB=AC. Vậy ∆ABC cân tại A. HocTot.Nam.Name.Vn
|