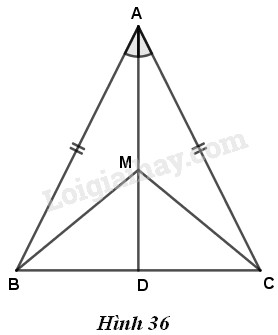
Bài 38 trang 86 Vở bài tập toán 7 tập 2Giải bài 38 trang 86 VBT toán 7 tập 2. Cho tam giác ABC cân tại A. Trên đường phân giác AD, lấy điểm M (h.36) a) Chứng minh... Đề bài Cho tam giác ABC cân tại A. Trên đường phân giác AD, lấy điểm M (h.36) a) Chứng minh ΔABM=ΔACM; b) So sánh các góc MBC và MCB; c) Chứng minh MD là một đường phân giác của tam giác MBC.
Phương pháp giải - Xem chi tiết Vận dụng kiến thức về tính chất ba đường phân giác trong tam giác và cách chứng minh tam giác bằng nhau. Lời giải chi tiết
a) Xét hai tam giác ABM và ACM. Ta có AB=AC (vì tam giác ABC cân tại A), ^BAM=^CAM (vì AD là đường phân giác xuất phát từ đỉnh A) và AM là cạnh chung. Vậy ΔABM=ΔACM (c.g.c) b) Theo câu a, ΔABM=ΔACM nên BM=CM (cặp cạnh tương ứng), nghĩa là ΔMBC cân tại M, suy ra ^MBC=^MCB. c) Ta có: Trong một tam giác cân, đường phân giác xuất phát từ đỉnh đối diện với đáy đồng thời là đường trung tuyến nên từ giả thiết AD là đường phân giác của góc A, ta suy ra AD là đường trung tuyến của ΔABC tức là BD=DC, hay MD là đường trung tuyến của ΔBMC. Suy ra MD là một đường phân giác của ΔMBC. Lưu ý : Bài [39] chính là câu a) và câu b) của bài này. HocTot.Nam.Name.Vn
|