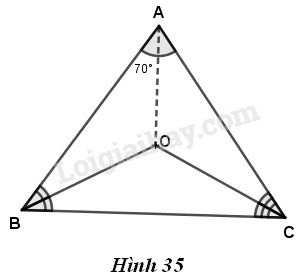
Bài 37 trang 85 Vở bài tập toán 7 tập 2Giải bài 37 trang 85 VBT toán 7 tập 2. Cho tam giác ABC có góc A = 70 độ. Gọi Gọi O là giao điểm của hai đường phân giác xuất phát từ B và C (h.35)... Đề bài Cho tam giác ABC có ˆA=70∘. Gọi O là giao điểm của hai đường phân giác xuất phát từ B và C (h.35). a) Tính góc BOC; b) Kẻ tia AO. Hãy tính góc BAO; c) Điểm O có cách đều ba cạnh của tam giác ABC hay không? Tại sao?
Phương pháp giải - Xem chi tiết Vận dụng kiến thức về tính chất ba đường phân giác trong tam giác và định lí tổng ba góc trong một tam giác. Lời giải chi tiết
a) Trong tam giác BOC, ta có ^BOC=180∘−(ˆB2+ˆC2) Mặt khác, trong tam giác ABC, ta có ˆB+ˆC=180∘−ˆA =180∘−70∘=110∘. Từ đó : ˆB2+ˆC2=ˆB+ˆC2=11002=55∘ Vậy ^BOC=180∘−55∘=125∘ b) Trong một tam giác, ba đường phân giác cùng đi qua một điểm nên tia phân giác góc A phải đi qua điểm chung là O của hai tia phân giác góc B và góc C nói cách khác, AO là tia phân giác của góc A. Vậy ^BAO=35∘. c) Vì O là điểm chung của ba đường phân giác trong tam giác ABC nên O cách đều ba cạnh của tam giác ABC. HocTot.Nam.Name.Vn
|