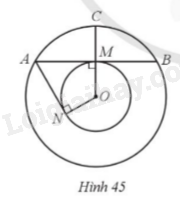
Giải bài 41 trang 121 sách bài tập toán 9 - Cánh diều tập 1

Đề bài

Cho hai đường tròn (O; R) và (O; 2R). Một dây cung AB của đường tròn (O; 2R) tiếp xúc với đường tròn (O; R) tại M. Kẻ tiếp tuyến thứ hai AN của đường tròn (O; R). Gọi S₁ là diện tích của hình tạo bởi cung ACB và dây AB của đường tròn (O; 2R), S₂ là diện tích của hình tạo bởi hai tiếp tuyến AM, AN và cung nhỏ MN của đường tròn (O; R) và S₃ là diện tích của hình tròn (O; R) (Hình 45). Chứng minh S₁ + S₂ = S_3.

 

Lời giải chi tiết

Vì AB tiếp xúc với (O;R) tại M nên AB là tiếp tuyến của (O;R), do đó \(OC \bot AB\) tại M hay \(\widehat {AMO} = \widehat {BMO} = 90^\circ \).

Áp dụng định lý Pythagore trong tam giác AMO vuông tại M có \(AM = \sqrt {A{O^2} - M{O^2}}  = \sqrt {{{\left( {2R} \right)}^2} - {R^2}}  = R\sqrt 3 \)

Ta lại có \(\cos \widehat {AOM} = \frac{{OM}}{{OA}} = \frac{R}{{2R}} = \frac{1}{2}\) suy ra \(\widehat {AOM} = 60^\circ \).

Xét tam giác OAM và tam giác OBM có:

\(OA = OB\left( { = 2R} \right)\);

OM chung;

\(\widehat {AMO} = \widehat {BMO} = 90^\circ \)

Suy ra \(\Delta OAM = \Delta OBM\) (cạnh huyền – cạnh góc vuông)

Do đó \(AM = BM = \frac{{AB}}{2}\) và \(\widehat {AOM} = \widehat {BOM} = \frac{{\widehat {AOB}}}{2}\)

Suy ra \(AB = 2AM = 2R\sqrt 3 \) và \(\widehat {AOB} = 2\widehat {AOM} = 2.60^\circ  = 120^\circ \).

Do AM, AN là 2 tiếp tuyến của (O;R) nên \(\widehat {AOM} = \widehat {AON} = \frac{{\widehat {MON}}}{2}\) hay \(\widehat {MON} = 2\widehat {AOM} = 2.60^\circ  = 120^\circ \).

Xét tam giác OMA và tam giác ONA có:

OA chung;

\(OM = ON\left( { = R} \right)\);

\(AM = AN\) (tính chất 2 tiếp tuyến cắt nhau)

Suy ra \(\Delta OAM = \Delta OAN\)(c.c.c), nên \({S_{\Delta OAM}} = {S_{\Delta OAN}}\)

Ta có: S₁ = diện tích quạt tròn AOB – diện tích \(\Delta OAB\)

Hay \({S_1} = \frac{{\pi {{\left( {2R} \right)}^2}n}}{{360}} - \frac{{OM.AB}}{2}\)\( = \frac{{\pi 4{R^2}.120}}{{360}} - \frac{{R.2R\sqrt 3 }}{2}\)\( = {R^2}\left( {\frac{{4\pi }}{3} - \sqrt 3 } \right)\)

S₂ = diện tích \(\Delta OAM\) + diện tích tam giác \(\Delta OAN\) - diện tích quạt tròn OMN

Hay S₂ = 2. diện tích \(\Delta OAM\) - diện tích quạt tròn OMN

Do đó \({S_2} = 2.\frac{{AM.OM}}{2} - \frac{{\pi {R^2}.n}}{{360}}\)\( = 2.\frac{{R\sqrt 3 .R}}{2} - \frac{{\pi {R^2}.120^\circ }}{{360}}\)\( = {R^2}\left( {\sqrt 3  - \frac{\pi }{3}} \right)\)

S₃ = diện tích hình tròn (O;R) \( = \pi {R^2}\)

Ta có \({S_1} + {S_2} = {R^2}\left( {\frac{{4\pi }}{3} - \sqrt 3 } \right) + {R^2}\left( {\sqrt 3  - \frac{\pi }{3}} \right) = \pi {R^2} = {S_3}\) (đpcm)