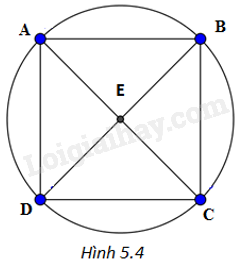
Giải bài 4 trang 99 vở thực hành Toán 9Cho hình vuông ABCD có E là giao điểm của hai đường chéo. a) Chứng minh rằng có một đường tròn đi qua bốn điểm A, B, C và D. Xác định tâm đối xứng và chỉ ra hai trục đối xứng của đường tròn đó. b) Tính bán kính của đường tròn ở câu a, biết rằng hình vuông có cạnh bằng 3cm. Tổng hợp Đề thi vào 10 có đáp án và lời giải Toán - Văn - Anh Đề bài Cho hình vuông ABCD có E là giao điểm của hai đường chéo. a) Chứng minh rằng có một đường tròn đi qua bốn điểm A, B, C và D. Xác định tâm đối xứng và chỉ ra hai trục đối xứng của đường tròn đó. b) Tính bán kính của đường tròn ở câu a, biết rằng hình vuông có cạnh bằng 3cm. Phương pháp giải - Xem chi tiết a) + Chứng minh \(AE = EB = EC = ED\) nên A, B, C, D nằm trên đường tròn tâm E, bán kính AE. + Hai đường chéo đi qua E nên AC và BD là hai trục đối xứng của đường tròn đó. b) Áp dụng định lí Pythagore vào tam giác ABC vuông tại B, từ đó tính được AC. Lời giải chi tiết (H.5.4)
a) Do ABCD là hình vuông nên \(AC = BD\) (hai đường chéo bằng nhau), \(AE = EB = EC = ED\) (nửa đường chéo). Do đó, A, B, C, D nằm trên đường tròn tâm E, bán kính AE. Hai đường chéo đi qua E nên AC và BD là hai trục đối xứng của đường tròn đó. b) Do ABC là tam giác vuông tại B, có \(AB = BC = 3cm\) nên theo định lí Pythagore, ta được \(A{C^2} = A{B^2} + B{C^2} = 18\), suy ra \(AC = 3\sqrt 2 \)cm. Vậy bán kính của đường tròn tâm E là \(AE = \frac{{AC}}{2} = \frac{{3\sqrt 2 }}{2}\left( {cm} \right)\).
|