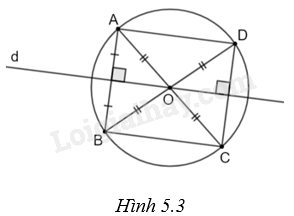
Giải bài 3 trang 99 vở thực hành Toán 9Cho đường tròn (O), đường thẳng d đi qua O và điểm A thuộc (O) nhưng không thuộc d. Gọi B là điểm đối xứng với A qua d; C và D lần lượt là điểm đối xứng với A và B qua O. a) Ba điểm B, C và D có thuộc (O) không? Vì sao? b) Chứng minh tứ giác ABCD là hình chữ nhật. c) Chứng minh rằng C và D đối xứng với nhau qua d. Tổng hợp Đề thi vào 10 có đáp án và lời giải Toán - Văn - Anh Đề bài Cho đường tròn (O), đường thẳng d đi qua O và điểm A thuộc (O) nhưng không thuộc d. Gọi B là điểm đối xứng với A qua d; C và D lần lượt là điểm đối xứng với A và B qua O. a) Ba điểm B, C và D có thuộc (O) không? Vì sao? b) Chứng minh tứ giác ABCD là hình chữ nhật. c) Chứng minh rằng C và D đối xứng với nhau qua d. Phương pháp giải - Xem chi tiết a) Tâm của đường tròn là tâm đối xứng của nó; đường thẳng đi qua tâm của đường tròn là một trục đối xứng của nó. b) + Chứng minh O là trung điểm của AC và BD nên tứ giác ABCD là hình bình hành. + Chứng minh \(AC = BD\) nên hình bình hành ABCD là hình chữ nhật. c) + Chứng minh AB//CD, do đó d là trung trực của AB cũng là đường trung trực của CD. + Suy ra, C và D đối xứng với nhau qua d. Lời giải chi tiết (H.5.3)
a) Vì d là một trục đối xứng của đường tròn và B đối xứng với A qua d nên từ \(A \in \left( O \right)\) suy ra \(B \in \left( O \right)\). Lại có O là tâm đối xứng của đường tròn và C, D lần lượt là điểm đối xứng với A, B qua O nên từ \(A,B \in \left( O \right)\) suy ra \(C,D \in \left( O \right)\). Vậy ba điểm B, C và D có thuộc (O). b) Vì C đối xứng với A qua O nên O là trung điểm của AC. Vì D đối xứng với B qua O nên O là trung điểm của BD. Tứ giác ABCD có hai đường chéo AC, BD và O là trung điểm của AC, BD nên ABCD là hình bình hành. Lại có \(AC = BD\) (cùng bằng đường kính của (O)). Do đó, hình bình hành ABCD là hình chữ nhật. c) Vì B đối xứng với A đến d nên d là đường trung trực của AB. Hình chữ nhật ABCD có AB//CD nên d cũng là đường trung trực của CD. Do đó C và D đối xứng với nhau qua d.
|