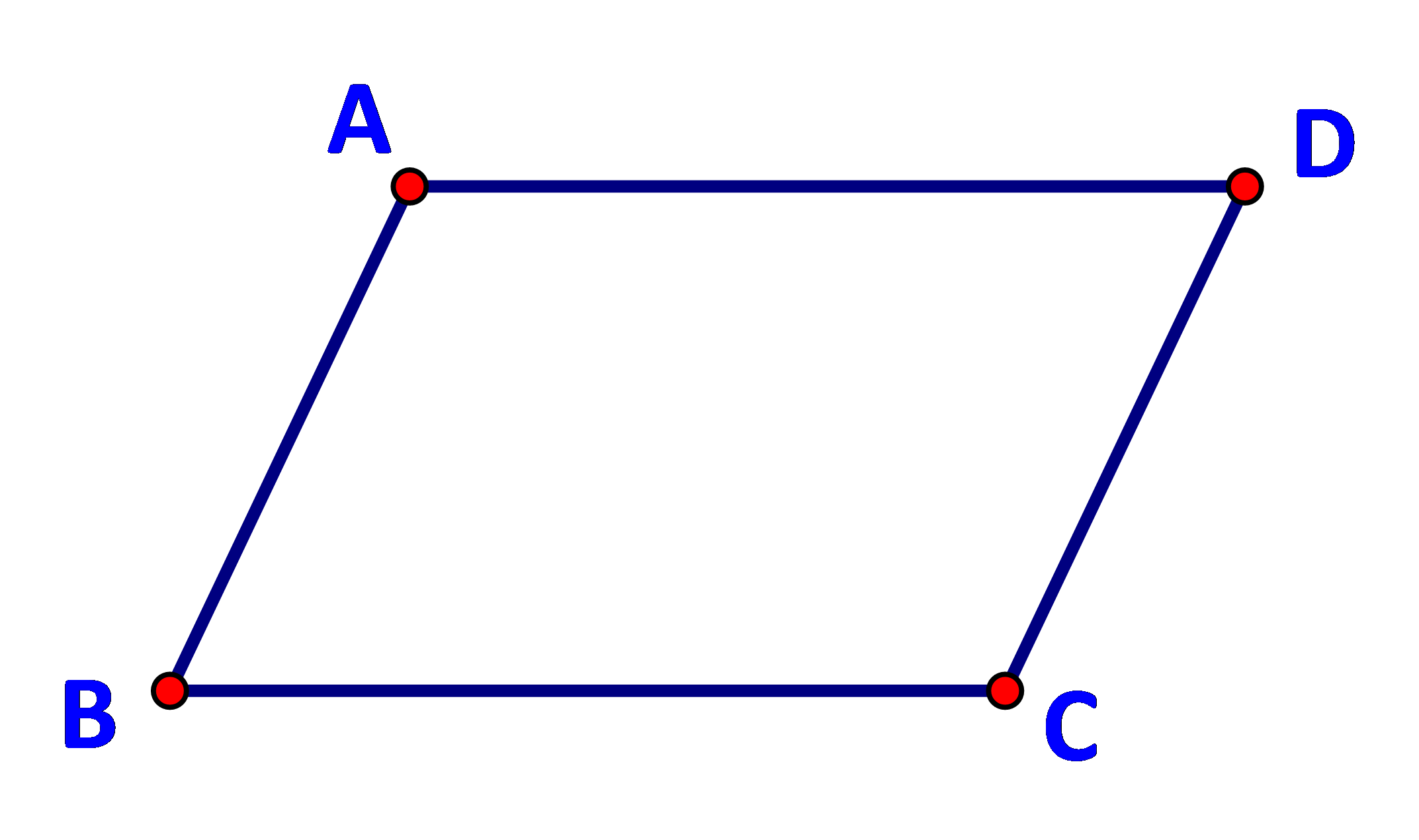
Giải bài 4 trang 87 SGK Toán 10 tập 1 – Cánh diềuCho hình hình hành ABCD, gọi O là giao điểm của AC và BD. Các khảng định sau đúng hay sai? Tổng hợp đề thi học kì 2 lớp 10 tất cả các môn - Cánh diều Toán - Văn - Anh - Lí - Hóa - Sinh - Sử - Địa... Đề bài Cho hình hình hành ABCD, gọi O là giao điểm của AC và BD. Các khảng định sau đúng hay sai? a) \(|\overrightarrow {AB} + \overrightarrow {AD} |\; = \;|\overrightarrow {AC} |\) b) \(\overrightarrow {AB} + \overrightarrow {BD} = \overrightarrow {CB} \) c) \(\overrightarrow {OA} + \overrightarrow {OB} = \overrightarrow {OC} + \overrightarrow {OD} \) Phương pháp giải - Xem chi tiết Nhắc lại: +) quy tắc hình bình hành: \(\overrightarrow {AB} + \overrightarrow {AD} = \overrightarrow {AC} \) với ABCD là hình bình hành. +) Tổng hai vecto: \(\overrightarrow {AB} + \overrightarrow {BC} = \overrightarrow {AC} \)\( \Leftrightarrow \overrightarrow {AC} - \overrightarrow {AB} = \overrightarrow {BC} \) với 3 điểm A, B, C bất kì. +) Vecto đối: \(\overrightarrow {BA} = - \overrightarrow {AB} \) Lời giải chi tiết a) Theo quy tắc hình bình hành ta có: \(\overrightarrow {AB} + \overrightarrow {AD} = \overrightarrow {AC} \) \( \Rightarrow |\overrightarrow {AB} + \overrightarrow {AD} |\; = \;|\overrightarrow {AC} |\) Vậy mệnh đề này đúng. b) Ta có: \(\overrightarrow {AB} + \overrightarrow {BD} = \overrightarrow {AD} = \overrightarrow {BC} \ne \overrightarrow {CB} \) Vậy mệnh đề này sai. c) Ta có: \(\overrightarrow {OA} + \overrightarrow {OB} = \overrightarrow {OC} + \overrightarrow {OD} \)\( \Leftrightarrow \overrightarrow {OA} - \overrightarrow {OD} + \overrightarrow {OB} - \overrightarrow {OC} = \overrightarrow {0} \Leftrightarrow \overrightarrow {DA} + \overrightarrow {CB} =\overrightarrow {0}\Leftrightarrow 2\overrightarrow {CB} =\overrightarrow {0} \) Vậy mệnh đề này sai.
|