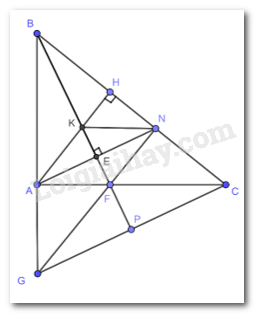
Giải Bài 4 trang 84 SGK Toán 7 tập 2 - Chân trời sáng tạoCho tam giác ABC vuông tại A (AB < AC). Trên cạnh BC lấy điểm N sao cho BA = BN Tổng hợp đề thi học kì 2 lớp 7 tất cả các môn - Chân trời sáng tạo Toán - Văn - Anh - Khoa học tự nhiên... Đề bài Cho tam giác ABC vuông tại A (AB < AC). Trên cạnh BC lấy điểm N sao cho BA = BN. Kẻ (E ∈ AN). a) Chứng minh rằng BE là tia phân giác của giác ABN. b) Kẻ đường cao AH của tam giác ABC. Gọi K là giao điểm của BH với CE. Chứng minh rằng NK // CA. c) Đường thẳng BK cắt AC tại F. Gọi G là giao điểm của đường thẳng AB với NF. Chứng minh rằng tam giác GBC cân. Video hướng dẫn giải Phương pháp giải - Xem chi tiết a) Ta chứng minh bằng cách chứng minh 2 tam giác BAF và BNF bằng nhau . b) Ta chứng minh NK song song với CA do có 2 góc so le trong bằng nhau c) Ta chứng minh góc BGC bằng góc BCG Lời giải chi tiết
a) Xét và có : BA = BN (giả thiết) BF cạnh chung (cạnh huyền-cạnh góc vuông) (góc tương ứng) BE là phân giác của góc ABN b) Vì K là giao của 2 đường cao K là trực tâm tam giác ABN KN vuông góc với AB(1) Vì CA vuông góc với AB ( tam giác ABC vuông tại A)(2) Từ (1) và (2) KN song song với CA (quan hệ cùng vuông góc với 1 đường) c) Ta có do có : BF cạnh chung BN = BA (2 góc tương ứng). Mà Ta có CA và GN là 2 đường cao của tam giác GBC F là trực tâm của tam giác GBC BF vuông góc với GC tại P Xét và ta có : BP cạnh chung (2 cạnh tương ứng) Tam giác GBC cân tại B
|