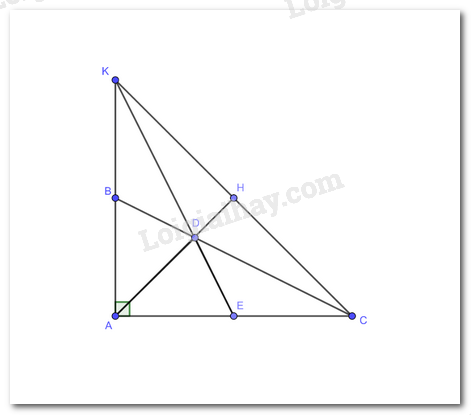
Giải Bài 7 trang 84 SGK Toán 7 tập 2 - Chân trời sáng tạo

Đề bài

Cho tam giác ABC vuông tại A có AB = $\dfrac{1}{2}$AC, AD là tia phân giác $\widehat {BAC}$(D ∈ BC). Gọi E là trung điểm của AC.

a) Chứng minh rằng DE = DB

b) AB cắt DE tại K. Chứng minh rằng tam giác DCK cân và B là trung điểm của đoạn thẳng AK.

c) AD cắt CK tại H. Chứng minh rằng AH$\bot$KC. 

Lời giải chi tiết

a) Xét $\Delta$BAD và $\Delta$EAD có :

AD là cạnh chung

AB = AE =$\dfrac{1}{2}$AC

$\widehat {BAD} = \widehat {EAD}$(do AD là phân giác góc A)

$\Rightarrow \Delta BAD = \Delta EAD$(c-g-c)

$\Rightarrow$DE = DB (cạnh tương ứng) và $\widehat {ABD} = \widehat {AED}$(góc tương ứng)

b) Xét $\Delta$KAE và $\Delta$CAB có :

AE = AB

$\widehat {ABD} = \widehat {AED}$(chứng minh a)

Góc A chung

$\Rightarrow \Delta KAE = \Delta CAB$(g-c-g)

$\Rightarrow$KE = CB (cạnh tương ứng)

Mà KE = ED + DK và CB = BD + DC

$\Rightarrow$KE – ED = CB – BD $\Rightarrow$DK = DC

$\Rightarrow$$\Delta DCK$cân tại D

+) Xét $\Delta$KDB và $\Delta$CDE có :

DB = DE

DK = DC

$\widehat {KDB} = \widehat {CDE}$(2 góc đối đỉnh)

$\Rightarrow \Delta KDB = \Delta CDE$(c-g-c)

$\Rightarrow$KB = EC $\Rightarrow$ KB = AB (do cùng = EC) $\Rightarrow$B là trung điểm AK

c) Vì $\Delta KAE$ = $\Delta CAB$ (chứng minh trên)

$\Rightarrow$AK = AC (cạnh tương ứng)

$\Rightarrow$$\Delta$AKC vuông cân tại A

Mà AD là phân giác góc A nên AD sẽ vừa là phân giác vừa là đường cao của $\Delta$AKC

$\Rightarrow$AD$\bot$KC

$\Rightarrow$AH$\bot$KC (do H $in$ AD)