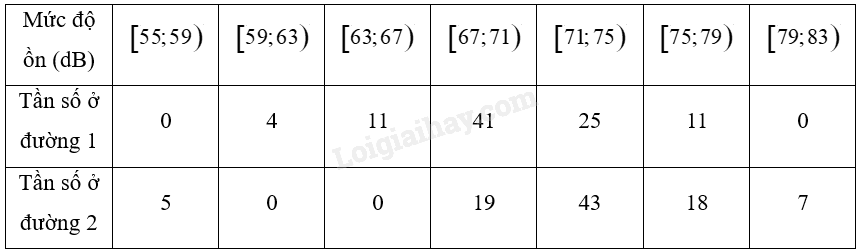
Giải bài 4 trang 110 sách bài tập toán 12 - Chân trời sáng tạo

Đề bài

Một nhóm nghiên cứu đã đo mức độ ồn của các phương tiến giao thông trên hai đường phố vào một ngày trong tuần, trong khoảng thời gian từ 5 giờ 30 phút đến 10 giờ 10 phút. Người ta thực đã thực hiện 92 lần đo ở mỗi con đường vào những khoảng thời gian như nhau. Kết quả thống kê được ghi lại như trong bảng sau:

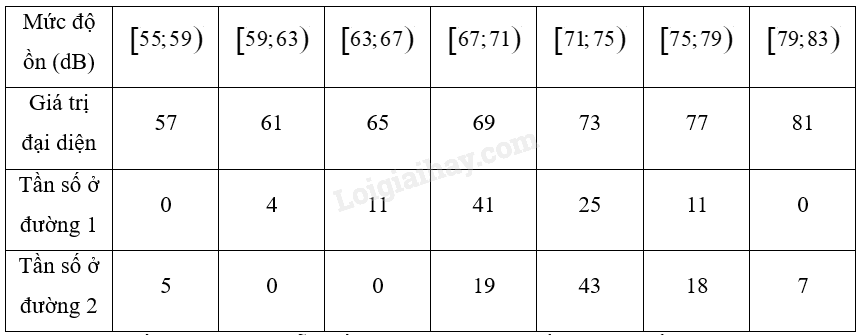
Hãy so sánh độ phân tán mức độ ồn của các phương tiện giao thông ở hai đường phố trên:

a) theo khoảng biến thiên;

b) theo khoảng tứ phân vị;

c) theo phương sai.

Lời giải chi tiết

Ta có bảng sau:

a) Khoảng biến thiên của mẫu số liệu ghép nhóm về mức độ ồn trên đường I là: \({R_I} = 79 - 59 = 20\left( {dB} \right)\).

Khoảng biến thiên của mẫu số liệu ghép nhóm về mức độ ồn trên đường II là: \({R_{II}} = 83 - 55 = 28\left( {dB} \right)\).

Do đó, nếu so sánh theo khoảng biến thiên, mức độ ồn trên đường II phân tán hơn trên đường I.

b) • Tứ phân vị của mẫu số liệu ghép nhóm về mức độ ồn trên đường I:

Cỡ mẫu: \({n_I} = 4 + 11 + 41 + 25 + 11 = 92\)

Gọi \({x_1};{x_2};...;{x_{92}}\) là mẫu số liệu gốc gồm mức độ ồn trên đường I theo thứ tự không giảm.

Tứ phân vị thứ nhất của mẫu số liệu gốc là \(\frac{1}{2}\left( {{x_{23}} + {x_{24}}} \right) \in \left[ {67;71} \right)\). Do đó tứ phân vị thứ nhất của mẫu số liệu ghép nhóm là:

\({Q_{I1}} = 67 + \frac{{\frac{{1.92}}{4} - \left( {4 + 11} \right)}}{{41}}\left( {71 - 67} \right) = \frac{{2779}}{{41}}\)

Tứ phân vị thứ ba của mẫu số liệu gốc là \(\frac{1}{2}\left( {{x_{69}} + {x_{71}}} \right) \in \left[ {71;75} \right)\). Do đó tứ phân vị thứ ba của mẫu số liệu ghép nhóm là:

\({Q_{I3}} = 71 + \frac{{\frac{{3.92}}{4} - \left( {4 + 11 + 41} \right)}}{{25}}\left( {75 - 71} \right) = \frac{{1827}}{{25}}\)

Khoảng tứ phân vị của mẫu số liệu ghép nhóm là:

\(\Delta {Q_I} = {Q_{I3}} - {Q_{I3}} = \frac{{1827}}{{25}} - \frac{{2779}}{{41}} = \frac{{5432}}{{1025}} \approx 5,3\left( {dB} \right)\).

• Tứ phân vị của mẫu số liệu ghép nhóm về mức độ ồn trên đường II:

Cỡ mẫu: \({n_{II}} = 5 + 19 + 43 + 18 + 7 = 92\)

Gọi \({x_1};{x_2};...;{x_{92}}\) là mẫu số liệu gốc gồm mức độ ồn trên đường II theo thứ tự không giảm.

Tứ phân vị thứ nhất của mẫu số liệu gốc là \(\frac{1}{2}\left( {{x_{23}} + {x_{24}}} \right) \in \left[ {67;71} \right)\). Do đó tứ phân vị thứ nhất của mẫu số liệu ghép nhóm là:

\({Q_{II1}} = 67 + \frac{{\frac{{1.92}}{4} - 5}}{{19}}\left( {71 - 67} \right) = \frac{{1345}}{{19}}\)

Tứ phân vị thứ ba của mẫu số liệu gốc là \(\frac{1}{2}\left( {{x_{69}} + {x_{71}}} \right) \in \left[ {75;79} \right)\). Do đó tứ phân vị thứ ba của mẫu số liệu ghép nhóm là:

\({Q_{II3}} = 75 + \frac{{\frac{{3.92}}{4} - \left( {5 + 19 + 43} \right)}}{{18}}\left( {75 - 71} \right) = \frac{{679}}{9}\)

Khoảng tứ phân vị của mẫu số liệu ghép nhóm là:

\(\Delta {Q_{II}} = {Q_{II3}} - {Q_{II3}} = \frac{{679}}{9} - \frac{{1345}}{{19}} = \frac{{796}}{{171}} \approx 4,65\left( {dB} \right)\).

Do đó, nếu so sánh theo khoảng tứ phân vị, mức độ ồn trên đường I phân tán hơn trên đường II.

c) • Phương sai của mẫu số liệu ghép nhóm về mức độ ồn trên đường I:

Số trung bình của mẫu số liệu ghép nhóm là:

\(\overline {{x_I}}  = \frac{{4.61 + 11.65 + 41.69 + 25.73 + 11.77}}{{92}} = \frac{{1615}}{{23}}\)

Phương sai của mẫu số liệu ghép nhóm đó là:

\(S_I^2 = \frac{1}{{92}}\left( {{{4.61}^2} + {{11.65}^2} + {{41.69}^2} + {{25.73}^2} + {{11.77}^2}} \right) - {\left( {\frac{{1615}}{{23}}} \right)^2} = \frac{{8048}}{{529}} \approx 15,21\)

• Phương sai của mẫu số liệu ghép nhóm về mức độ ồn trên đường II:

Số trung bình của mẫu số liệu ghép nhóm là:

\(\overline {{x_{II}}}  = \frac{{5.57 + 19.69 + 43.73 + 18.77 + 7.81}}{{92}} = \frac{{1672}}{{23}}\)

Phương sai của mẫu số liệu ghép nhóm đó là:

\(S_{II}^2 = \frac{1}{{92}}\left( {{{5.57}^2} + {{19.69}^2} + {{43.73}^2} + {{18.77}^2} + {{7.81}^2}} \right) - {\left( {\frac{{1672}}{{23}}} \right)^2} \approx 25,12\)

Do \(S_I^2 < S_{II}^2\) nên khi so sánh theo phương sai, mức độ ồn trên đường II phân tán hơn trên đường I.