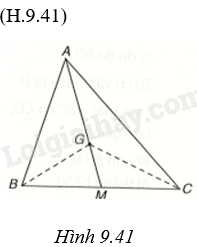
Giải bài 4 (9.35) trang 84, 85 vở thực hành Toán 7 tập 2Kí hiệu ({S_{ABC}}) là diện tích tam giác ABC. Gọi G là trọng tâm của tam giác ABC, M là trung điểm của BC. a) Chứng minh ({S_{GBC}} = frac{1}{3}{S_{ABC}}). Gợi ý. Sử dụng (GM = frac{1}{3}AM) để chứng minh ({S_{GBM}} = frac{1}{3}{S_{ABM}},{S_{GCM}} = frac{1}{3}{S_{ACM}}). b) Chứng minh ({S_{GCA}} = {S_{GAB}} = frac{1}{3}{S_{ABC}}). Nhận xét. Từ bài tập trên ta có: ({S_{GBC}} = {S_{GCA}} = {S_{GAB}} = frac{1}{3}{S_{ABC}}), điều này giúp ta cảm nhận tại sao có thể đặt thăng b Tổng hợp đề thi học kì 2 lớp 7 tất cả các môn - Kết nối tri thức Toán - Văn - Anh - Khoa học tự nhiên... Đề bài Kí hiệu \({S_{ABC}}\) là diện tích tam giác ABC. Gọi G là trọng tâm của tam giác ABC, M là trung điểm của BC. a) Chứng minh \({S_{GBC}} = \frac{1}{3}{S_{ABC}}\). Gợi ý. Sử dụng \(GM = \frac{1}{3}AM\) để chứng minh \({S_{GBM}} = \frac{1}{3}{S_{ABM}},{S_{GCM}} = \frac{1}{3}{S_{ACM}}\). b) Chứng minh \({S_{GCA}} = {S_{GAB}} = \frac{1}{3}{S_{ABC}}\). Nhận xét. Từ bài tập trên ta có: \({S_{GBC}} = {S_{GCA}} = {S_{GAB}} = \frac{1}{3}{S_{ABC}}\), điều này giúp ta cảm nhận tại sao có thể đặt thăng bằng miếng bìa hình tam giác trên giá nhọn đặt tại trọng tâm của tam giác đó. Phương pháp giải - Xem chi tiết a) Vì \(GM \) \(= \frac{1}{3}AM\), suy ra \({S_{GBM}} \) \(= \frac{1}{3}{S_{ABM}},{S_{GCM}} \) \(= \frac{1}{3}{S_{ACM}}\). Suy ra: \({S_{GBC}} \) \(= {S_{BGM}} + {S_{CGM}} \) \(= \frac{1}{3}{S_{ABM}} + \frac{1}{3}{S_{ACM}} \) \(= \frac{1}{3}\left( {{S_{ABM}} + {S_{ACM}}} \right) \) \(= \frac{1}{3}{S_{ABC}}\) b) + Tương tự phần a ta có: \({S_{GAC}} \) \(= {S_{CGN}} + {S_{AGN}} \) \(= \frac{1}{3}{S_{BCN}} + \frac{1}{3}{S_{ABN}} \) \(= \frac{1}{3}{S_{ABC}}\), \({S_{GAB}} \) \(= {S_{BGP}} + {S_{AGP}} \) \(= \frac{1}{3}{S_{BCP}} + \frac{1}{3}{S_{APC}} \) \(= \frac{1}{3}{S_{ABC}}\). Lời giải chi tiết
a) Ta có \({S_{GBC}} \) \(= {S_{BGM}} + {S_{CGM}}\). Vì G là trọng tâm của tam giác ABC nên \(GM \) \(= \frac{1}{3}AM\), suy ra \({S_{GBM}} \) \(= \frac{1}{3}{S_{ABM}},{S_{GCM}} \) \(= \frac{1}{3}{S_{ACM}}\). Suy ra: \({S_{GBC}} \) \(= {S_{BGM}} + {S_{CGM}} \) \(= \frac{1}{3}{S_{ABM}} + \frac{1}{3}{S_{ACM}} \) \(= \frac{1}{3}\left( {{S_{ABM}} + {S_{ACM}}} \right) \) \(= \frac{1}{3}{S_{ABC}}\). b) Tương tự \(GN \) \(= \frac{1}{3}BN\) nên \({S_{GAC}} \) \(= {S_{CGN}} + {S_{AGN}} \) \(= \frac{1}{3}{S_{BCN}} + \frac{1}{3}{S_{ABN}} \) \(= \frac{1}{3}\left( {{S_{BCN}} + {S_{ABN}}} \right) \) \(= \frac{1}{3}{S_{ABC}}\) Vì \(GP \) \(= \frac{1}{3}CP\) nên \({S_{GAB}} \) \(= {S_{BGP}} + {S_{AGP}} \) \(= \frac{1}{3}{S_{BCP}} + \frac{1}{3}{S_{APC}} \) \(= \frac{1}{3}\left( {{S_{BCP}} + {S_{APC}}} \right) \) \(= \frac{1}{3}{S_{ABC}}\) Vậy \({S_{GBC}} \) \(= {S_{GCA}} \) \(= {S_{GAB}} \) \(= \frac{1}{3}{S_{ABC}}\)
|