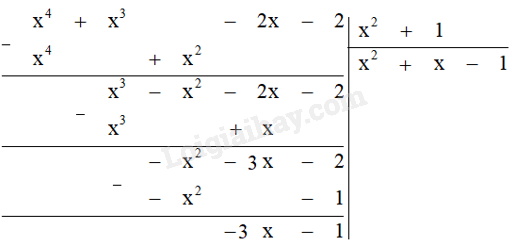Giải bài 4 (7.44) trang 53, 54 vở thực hành Toán 7 tập 2Cho đa thức (A = {x^4} + {x^3} - 2x - 2). a) Tìm đa thức B sao cho (A + B = {x^3} + 3x + 1). b) Tìm đa thức C sao cho (A - C = {x^5}). c) Tìm đa thức D sao cho (D = left( {2{x^2} - 3} right).A). d) Tìm đa thức P sao cho (A = left( {x + 1} right).P). e) Có hay không một đa thức Q sao cho (A = left( {{x^2} + 1} right).Q)? Đề bài Cho đa thức \(A = {x^4} + {x^3} - 2x - 2\). a) Tìm đa thức B sao cho \(A + B = {x^3} + 3x + 1\). b) Tìm đa thức C sao cho \(A - C = {x^5}\). c) Tìm đa thức D sao cho \(D = \left( {2{x^2} - 3} \right).A\). d) Tìm đa thức P sao cho \(A = \left( {x + 1} \right).P\). e) Có hay không một đa thức Q sao cho \(A = \left( {{x^2} + 1} \right).Q\)? Phương pháp giải - Xem chi tiết a) Vì \(A + B = {x^3} + 3x + 1\) nên \(B = \left( {{x^3} + 3x + 1} \right) - A\), từ đó tìm được B. b) Vì \(A - C = {x^5}\) nên \(C = A - {x^5} = \left( {{x^4} + {x^3} - 2x - 2} \right) - {x^5}\), từ đó tìm được C. c) Vì \(D = \left( {2{x^2} - 3} \right).A\) nên \(D = \left( {2{x^2} - 3} \right)\left( {{x^4} + {x^3} - 2x - 2} \right)\), từ đó tìm được D. d) Vì \(A = \left( {x + 1} \right).P\) nên \(B = \left( {{x^3} + 3x + 1} \right) - A\), phép chia A:P phải là phép chia hết và P là thương trong phép chia đó. e) Ta tìm Q bằng cách đặt tính chia A cho \({x^2} + 1\), từ đó rút ra kết luận. Lời giải chi tiết a) Muốn \(A + B = {x^3} + 3x + 1\) thì ta cần có \(B = \left( {{x^3} + 3x + 1} \right) - A\) \( = \left( {{x^3} + 3x + 1} \right) - \left( {{x^4} + {x^3} - 2x - 2} \right)\) \( = {x^3} + 3x + 1 - {x^4} - {x^3} + 2x + 2\) Rút gọn ta được \(B = - {x^4} + 5x + 3\). b) Muốn \(A - C = {x^5}\) thì ta cần có \(C = A - {x^5} = \left( {{x^4} + {x^3} - 2x - 2} \right) - {x^5}\) Rút gọn C ta có: \(C = - {x^5} + {x^4} + {x^3} - 2x - 2\). c) Ta có: \(D = \left( {2{x^2} - 3} \right)\left( {{x^4} + {x^3} - 2x - 2} \right)\) \( = 2{x^2}\left( {{x^4} + {x^3} - 2x - 2} \right) - 3\left( {{x^4} + {x^3} - 2x - 2} \right)\) \( = \left( {2{x^6} + 2{x^5} - 4{x^3} - 4{x^2}} \right) - \left( {3{x^4} + 3{x^3} - 6x - 6} \right)\) \( = 2{x^6} + 2{x^5} - 3{x^4} - 7{x^3} - 4{x^2} + 6x + 6\) d) Để có \(A = \left( {x + 1} \right).P\), phép chia A:P phải là phép chia hết và P là thương trong phép chia đó. Ta hãy tìm P bằng cách đặt tính chia A cho \(x + 1\) như sau:
Vậy \(P = {x^3} - 2\). e) Để có \(A = \left( {{x^2} + 1} \right).Q\), phép chia \(A:\left( {{x^2} + 1} \right)\) phải là phép chia hết và Q là thương trong phép chia đó. Ta hãy tìm Q bằng cách đặt tính chia A cho \({x^2} + 1\) như sau:
Ta được đa thức dư là \( - 3x - 1\). Vậy A không chia hết cho \({x^2} + 1\). Điều đó chứng tỏ không tồn tại một đa thức Q sao cho \(A = \left( {{x^2} + 1} \right).Q\).
|