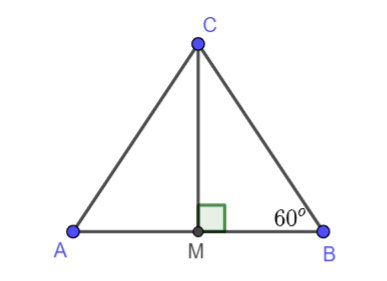
Giải bài 4 (4.32) trang 77 vở thực hành Toán 7

Đề bài

Bài 4 (4.32). Cho tam giác MBC vuông tại M có $\widehat B = {60^o}$. Gọi A là điểm nằm trên tia đối của tia MB sao cho MA = MB. Chứng minh rằng tam giác ABC là tam giác đều.

Lời giải chi tiết

GT	$\Delta MBC,\widehat M = {90^o},\widehat B = {60^o},MA = MB$ A thuộc tia đối của tia MB
KL	$\Delta ABC$đều.

Ta thấy hai tam giác MBC và MAC vuông tại M và có:

MB = MA (theo giả thiết)

MC là cạnh chung

Vậy $\Delta MBC = \Delta MAC$(hai cạnh góc vuông). Do đó $\widehat A = \widehat B = {60^o}$

Suy ra $\widehat C = {180^o} - \widehat A - \widehat B = {60^o}$

Vậy ABC là tam giác có ba góc bằng nhau nên đây là tam giác đều.