Bài 37 trang 92 SBT toán 8 tập 2

Đề bài

Cho tam giác $ABC$ có $\widehat A = 60^\circ$, $AB = 6cm, AC = 9cm$

a) Dựng tam giác đồng dạng với tam giác $ABC$ theo tỉ số đồng dạng $\displaystyle k = {1 \over 3}$

b) Hãy nêu một vài cách dựng khác và vẽ hình trong từng trường hợp cụ thể.

Lời giải chi tiết

a)

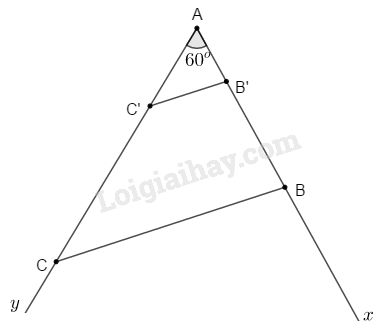
Cách dựng:

- Dựng $\widehat {xAy} = {60^o}$

- Trên tia $Ax$ lấy hai điểm $B$ và $B'$ sao cho $AB=6\,cm$ và $AB’ = 2cm.$

- Trên tia $Ay$ lấy điểm $C$ và $C'$ sao cho $AC=9cm$ và $AC’ = 3cm.$

- Nối $B$ với $C$, ta được $\Delta ABC$ thỏa mãn yêu cầu bài toán.

- Nối $B’$ với $C’$, khi đó $\Delta AB’C’$ là tam giác cần dựng.

Chứng minh:

Theo cách dựng, ta có:

$\displaystyle{{AB'} \over {AB}} = {2 \over 6} = {1 \over 3}$

$\displaystyle{{AC'} \over {AC}} = {3 \over 9} = {1 \over 3}$

$\Rightarrow\displaystyle {{AB'} \over {AB}} = {{AC'} \over {AC}} = {1 \over 3}$

Xét $∆ AB’C’$ và $∆ ABC$ có:

$\displaystyle {{AB'} \over {AB}} = {{AC'} \over {AC}} = {1 \over 3}$

$\widehat A$ chung

$\Rightarrow ∆ AB’C’$ đồng dạng $∆ ABC$ (c.g.c)

b) 

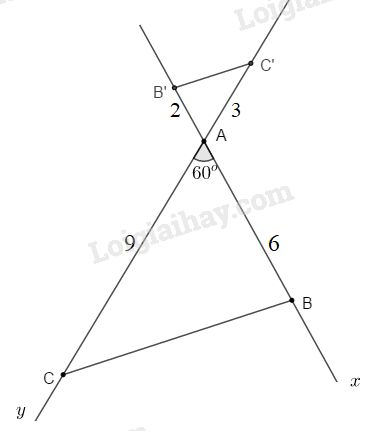
Cách dựng:

- Dựng $\widehat {xAy} = {60^o}$

- Trên tia $Ax$ lấy hai điểm $B$ sao cho $AB=6\,cm$.

- Trên tia $Ay$ lấy điểm $C$ sao cho $AC=9cm$.

- Nối $B$ với $C$, ta được $\Delta ABC$ thỏa mãn yêu cầu bài toán.

- Trên tia đối của tia $Ax$ dựng điểm $B’$ sao cho $AB’ = 2cm.$

- Trên tia đối của tia $Ay$ dựng điểm $C’$ sao cho $AC’ = 3cm.$

- Nối $B’$ với $C’$, khi đó $\Delta AB’C’$ là tam giác cần dựng.

Chứng minh:

Theo cách dựng, ta có:

$\displaystyle{{AB'} \over {AB}} = {2 \over 6} = {1 \over 3}$

$\displaystyle{{AC'} \over {AC}} = {3 \over 9} = {1 \over 3}$

$\Rightarrow\displaystyle {{AB'} \over {AB}} = {{AC'} \over {AC}} = {1 \over 3}$

Xét $∆ AB’C’$ và $∆ ABC$ có:

$\displaystyle {{AB'} \over {AB}} = {{AC'} \over {AC}} = {1 \over 3}$

$\widehat {B'AC'}=\widehat {BAC}$ (đối đỉnh)

$\Rightarrow ∆ AB’C’$ đồng dạng $∆ ABC$ (c.g.c)

HocTot.Nam.Name.Vn